Cho tam giác ABC cân tại A có \(\widehat{A}\) = 20o.Trên cạnh AB lấy điểm D sao cho AD = BC . Tính \(\widehat{BDC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực cua BC
Lại có : AB=AC(ABC can tai A)
=> A thuộc trung trực cua BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = góc BAC /2 = 20 độ/2=10 độ
tam giac ABC can tai A
=> goc CBA = goc BCA = (180 - goc BAC)/2= (180 - 20)/2 = 80 độ
lai co : goc MCA = goc ACB - goc MCB
goc MCB = 60 độ (Tg BCM đều)
Suy ra : goc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chung
CM=DA (cung bang BC)
goc MCA = goc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> goc CDA = goc CMA = 150 độ
Mat khac : goc CDA + goc BDC = 180 độ (2 goc ke bu)
suy ra : goc BDC = 30 độ
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực cua BC
Lại có : AB=AC(ABC can tai A)
=> A thuộc trung trực cua BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = góc BAC /2 = 20 độ/2=10 độ
tam giac ABC can tai A
=> goc CBA = goc BCA = (180 - goc BAC)/2= (180 - 20)/2 = 80 độ
lai co : goc MCA = goc ACB - goc MCB
goc MCB = 60 độ (Tg BCM đều)
Suy ra : goc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chung
CM=DA (cung bang BC)
goc MCA = goc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> goc CDA = goc CMA = 150 độ
Mat khac : goc CDA + goc BDC = 180 độ (2 goc ke bu)
suy ra : goc BDC = 30 độ

Sửa đầu bài chỗ AB= BC thì AD = BC mới lm đc:
trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực của BC
Lại có : AB=AC(ABC cân tại A)
=> A thuộc trung trực của BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = gốc BAC /2 = 20 độ/2=10 độ tam giác ABC cân tại A
=> góc CBA = góc BCA = (180 - gốc BAC)/2= (180 - 20)/2 = 80 độ
lại có : góc MCA = góc ACB - góc MCB góc MCB = 60 độ (Tg BCM đều)
Suy ra : góc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chúng CM=ĐA (cùng bằng BC)
góc MCA = góc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> góc CDA = góc CMA = 150 độ
Mặt khác :
góc CDA + góc BDC = 180 độ (2 góc kề bù)
suy ra : góc BDC = 30 độ


b) Ta có: AD+DC=AC(D nằm giữa A và C)
nên DC=AC-AD=3-1=2(cm)
Ta có: DE=AD(gt)
mà AD=1cm(cmt)
nên DE=1cm
Ta có: \(\dfrac{BD}{CD}=\dfrac{\sqrt{2}}{2}\)
\(\dfrac{DE}{DB}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Do đó: \(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)\(\left(=\dfrac{\sqrt{2}}{2}\right)\)
Xét ΔBDE và ΔCDB có
\(\dfrac{BD}{CD}=\dfrac{DE}{DB}\)(cmt)
\(\widehat{BDE}\) chung
Do đó: ΔBDE\(\sim\)ΔCDB(c-g-c)
a) Ta có: AD+DE+EC=AC
mà AD=DE=EC(gt)
nên \(AD=\dfrac{AC}{3}=\dfrac{3}{3}=1\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=1+1=2\)
hay \(BD=\sqrt{2}cm\)
Vậy: \(BD=\sqrt{2}cm\)

a. Xét tam giác ABC và tam giác ADE
AB=AD
BAC=DAE=90*
AC=AE
=> tam giác ABC= tam giác ADE(cgc)
=> BC=DE
b. Gọi giao điểm giữa ED và BC là H
Theo câu a, tam giác ABC= tam giác ADE(cgc) => ACB=AED
Xét tam giác ADE có ADE+AED+DAE=180*
Xét tam giác HDC có
HDC+HCD+DHC=180*
Mà ADE=HDC; AED=HCD
=> DAE=DHC=90*
=> DE vg BC
c. Gọi số đo góc B, C lần lượt là b,c
Do tam giác ABC vuông tại A=> B+C=90* => b+c=90*
Theo bài ra ta có: 4b=5c=> \(\frac{b}{5}=\frac{c}{4}=\frac{b+c}{5+4}=\frac{90}{9}=10\)
=> b=10.5=50*
=> ABC=50* => ADE=50*

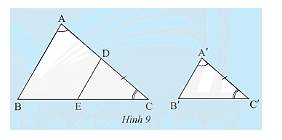
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).
Trên nửa mặt phẳng bờ BC dựng \(\Delta\)BCE đều
Xét \(\Delta\)BAE và \(\Delta\) CAE có:
AB = AC (\(\Delta\)ABC cân)
AE: chung
EB = EC (\(\Delta\)BCE đều)
\(\Rightarrow\)\(\Delta\)BAE = \(\Delta\) CAE (c.c.c)
\(\Rightarrow\)BAE = CAE (2 cạnh tương ứng)
\(\Rightarrow\)AE là phân giác BAC
\(\Rightarrow\)BAE = CAE = BAC : 2 = 20o : 2 = 10o
Vì \(\Delta\) ABC cân ở A \(\Rightarrow\)BCA = (180o - BAC) : 2 = 80o
Ta có: \(\Delta\)BCE đều \(\Rightarrow\)ECB = 60o
Có: ACE + ECB = ACB
\(\Rightarrow\)ACE = ACB - ECB = 80o - 60o = 20o
\(\Rightarrow\)ACE = CAD
Xét \(\Delta\)DAC và \(\Delta\)ECA có:
AC: chung
ACE = CAD (cmt)
EC = AD (= BC)
\(\Rightarrow\)\(\Delta\)DAC = \(\Delta\)ECA (c.g.c)
\(\Rightarrow\)EAC = ECA = 10o (2 góc tương ứng)
Ta có: BDC = DAC + ECA = 20o + 10o =30o
Vậy BDC = 30o