Một đa giác có n cạnh trong đó có một cạnh có độ dài bằng 1, độ dài các đường chéo là các số nguyên. Tìm tất cả các giá trị n có thể
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
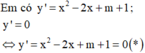
Để hàm số có hai điểm cực trị thỏa mãn đề bài ⇔ Phương trình (*) có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn x 1 > 0 ; x 2 > 0 và x 1 2 + x 2 2 = 5
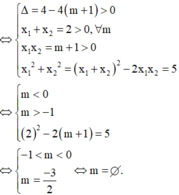

TH1: 2 cạnh nguyên tố đó là 2 cạnh góc vuông lần lượt: a;a+50a;a+50
Khi đó, cạnh huyền: a2+(a+50)2−−−−−−−−−−−√=2a2+100a+2500−−−−−−−−−−−−−−−√a2+(a+50)2=2a2+100a+2500
Với a=5 (loại).
Với a khác 5, có: a2≡1or4(mod5)→2a2+100a+2500≡2or3(mod5)a2≡1or4(mod5)→2a2+100a+2500≡2or3(mod5) kg là SCP.
Vậy TH này loại.
TH2: 1 cạnh huyền, 1 cạnh góc vuông: a;a+50a;a+50
Cạnh góc vuông còn lại: (a+50)2−a2−−−−−−−−−−−√=100a+2500−−−−−−−−−−√=10.a+25−−−−−√(a+50)2−a2=100a+2500=10.a+25
Đặt: a+25−−−−−√=t→a+25=t2⇔a=(t−5)(t+5)→t−5=1⇔t=6⇔a=11a+25=t→a+25=t2⇔a=(t−5)(t+5)→t−5=1⇔t=6⇔a=11 (đúng)
Vậy số đo 3 cạnh nhỏ nhất là: 11;60;6111;60;61 (11,61 nguyên tố)
Vậy đáp số giá trị nhỏ nhất của cạnh thứ 3: 60

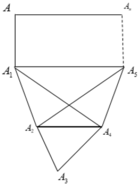
Nhận thấy: Hình vuông và hình ngũ giác đều thỏa mãn yêu cầu của bài toán
Ta chứng minh đa giác có số cạnh lớn hơn 5 không thỏa mãn yêu cầu của bài toán bằng phương pháp phản chứng.

là các cạnh của tứ giác nên tổng hai đường chéo lớn hơn tổng hai cạnh đối.

⇒ Giả thiết đưa ra là sai.
Vậy đa giác có số cạnh lớn hơn 5 thì không thỏa mãn yêu cầu bài.
