Câu cuối nè ;-;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Japanese cars is the most expensive car in the world
This exercise is not as easy as this one
Jack doesn't drives car more carefully than he does
He can play the best in the group
This hotel is the most comfortable in the city
The Pacific Ocean is the largest in the world

-Giao tiếp có văn hóa có ý nghĩa vô cùng quan trọng trong cuộc sống, đem lại niềm vui, hạnh phúc cho mình và mọi người xung quanh. Giúp mọi người biết tôn trọng bản thân, tôn trọng người khác, góp phần xây dựng xã hội đổi mới văn minh và tốt đẹp hơn.

Nhà tôi năm nay còn khôm có bánh tét hạt dưa :(((
Cho xin miếng đi :>

- Xã hội chia thành nhiều tầng lớp , tiêu biểu là : quyền quý , dân tự do , nô tì
- Tổ chúc lể hội , vui chơi , ca nhạc , ....
- Phong tục : ăn trầu , nhuộm răng , làm bánh chưng , bánh giầy , .....
Sáng nay mình thi rùi nhưng trúng đề 3 bài kia còn bài này ko có ![]()

Em đồng ý và Em nghĩ theo 2 hướng:
Thứ nhất, là đối với mấy anh chị cuối cấp như lớp 9 lớp 12 thì cần hoàn thiện 100% các môn chính, bài học cũng nhiều nên em nghĩ là nên bỏ các môn phụ đi và thay vào đó là các tiết tự học hoặc ôn tập thêm để các anh chị chuẩn bị tốt cho cuộc thi quan trọng hơn
Thứ 2 là đối với các khối còn lại :
Hiện này thì chương trình của mấy em lớp 6 phải học khá nhiều môn và nó khá rắc rối so với độ tuổi của các em là cần vui chơi nên cần miễn giảm bớt môn học chính khiến các em dễ nản và dẫn đến lười học vậy nên thay vào nhiều môn phụ hơn để các em hứng thú hơn nhiều í ạ.
Cfon các anh chị thì chúng ta nên cho các môn phụ là môn tự chọn(lựa chọn theo sự đồng thuận của mỗi lớp) vì các môn phụ thì phải thi, phải học, phải đánh giá chất lượng , phải luyện tập trong khi bài vở của các môn chính khá nhiều. Độ khó của các môn chính tăng lên thì các môn phụ cũng theo đà đó mà phát triển. Yêu cầu chất lượng, hiệu quả cũng cao hơn nên học sinh cảm thấy mệt vì phải học môn chính kèm theo 1 gánh nặng khác trên vai là làm sao để đạt các môn phụ.
Trước đây và bây giờ An-đrây-ca đã từng có một việc làm day dứt lương tâm của cậu.Để biết rõ hơn mời các bạn lắng nghe câu chuyện đó.Vài năm trước,An-đrây-ca có một người ông,ông của cậu bị một chứng bệnh rất nặng.Một buổi chiều nọ,ông của cậu nói với mẹ An-đrây ca:"Bố khó thở lắm !"...Mẹ liền thúc giục An-đrây-ca đi mua thuốc.Cậu bé vội vã chạy đi ngay,nhưng dọc đường cậu gặp những đứa bạn của mình đang chơi bóng đá rủ nhập cuộc.Chơi được một hồi,cậu sực nhớ ra lời mẹ dặn.Cậu vội chạy một mạch đến tiệm thuốc,nhưng...Đã quá muộn rồi,cậu chạy về,hốt hoảng khi thấy mẹ khóc nấc lên.Hóa ra ông đã qua đời,cậu ân hận tự trách: “Chỉ vì mình mải chơi bóng, mua thuốc về chậm mà ông chết".Cậu oà khóc và kể hết mọi chuyện cho mẹ nghe. Mẹ an ủi:" Không, con không có lỗi. Chẳng thuốc nào cứu nổi ông đâu, ông đã mất từ lúc con vừa ra khỏi nhà".Nhưng cậu lại không nghĩ thế,ngồi cạnh dưới gốc cây táo do ông vun trồng,cậu lại càng nức nở.Mãi sau này cậu vẫn nghĩ“Giá mình mua thuốc về ngay thì ông ngoại còn sống thêm được vài năm nữa!”.

 Mấy câu cuối nè giúp em đi =(???
Mấy câu cuối nè giúp em đi =(???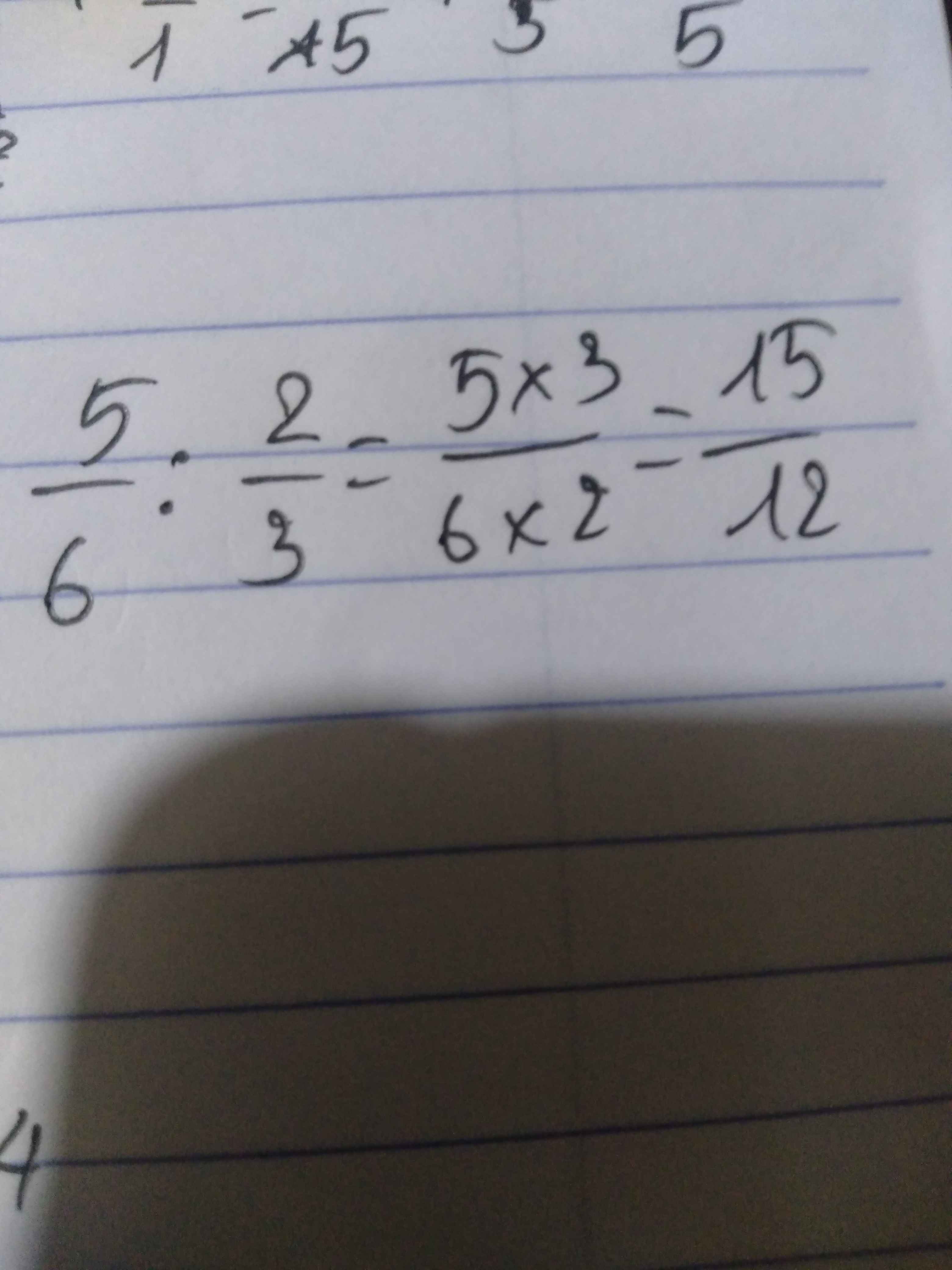


Nhận thấy vai trò a,b,c là như nhau nên giả sử a là số lớn nhất trong 3 số a,b,c
Khi đó ta xét 2 TH sau:
Nếu \(b\ge c\) thì khi đó: \(\hept{\begin{cases}a-b\ge0\\b-c\ge0\\c-a\le0\end{cases}}\)
\(\Rightarrow P=\left(a-b\right)\left(b-c\right)\left(c-a\right)\le0\)
Nếu \(b< c\) thì khi đó: \(\hept{\begin{cases}a-b>0\\b-c< 0\\c-a\le0\end{cases}}\)
\(\Rightarrow P=\left(a-b\right)\left(b-c\right)\left(c-a\right)\ge0\)
Áp dụng Bđt Cauchy ta có: \(\left(b-c\right)\left(c-a\right)\le\frac{\left(b-c+c-a\right)^2}{4}=\frac{\left(b-a\right)^2}{4}=\frac{\left(a-b\right)^2}{4}\)
\(\Rightarrow P=\left(a-b\right)\left(b-c\right)\left(c-a\right)\le\left(a-b\right)\cdot\frac{\left(a-b\right)^2}{4}=\frac{\left(a-b\right)^3}{4}\)
Vì \(\hept{\begin{cases}b\ge0\\a\le1\end{cases}}\) nên \(P\le\frac{\left(a-b\right)^3}{4}\le\frac{\left(1-0\right)^3}{4}=\frac{1}{4}\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}a=1\\b=0\\c=\frac{1}{2}\end{cases}}\) và các hoán vị
Qua hai TH trên vậy \(P_{max}=\frac{1}{4}\Leftrightarrow\hept{\begin{cases}a=1\\b=0\\c=\frac{1}{2}\end{cases}}\) và các hoán vị của chúng