\(\frac{x+3}{5}=\frac{2x+1}{4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_1)
![[CHUẨN NHẤT] Thế nào là hai phương trình tương đương (ảnh 2)](https://api.toploigiai.vn/storage/uploads/the-nao-la-hai-phuong-trinh-tuong-duong_2)
NT
0
S
1
C
15 tháng 2 2017
Thuật toán:
B1: Nhập a,b
B2:Nếu a< > 0 thì x=-a/b và kết thúc ngược lại thì đi tiếp
B3:Nếu b=0 thì phương trình vô số ngiệm ngược lại thì chương vô nghiệm và kết thúc thuật toán.
Viết chương trình:
Program PT_bac_nhat;
Var
a,b:Integer;
x:Real;
Begin
Writeln('GIAI PHUONG TRINH BAC NHAT');
Writeln(' aX + b = 0');
Write('-Nhap he so a= ');
Readln(a);
Write('-Nhap he so b= ');
Readln(b);
If a=0 Then
If b=0 Then
Writeln('+Phuong trinh vo dinh')
Else
Writeln('+Phuong trinh vo nghiem')
Else
Begin
x:=-b/a;
Writeln('+Nghiem cua phuong trinh X= ',x:0:6);
End;
Writeln;
Writeln(' Bam phim <Enter> de ket thuc');
Readln
End.
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
PT
1
CM
9 tháng 4 2019
Phương trình dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
Đáp án cần chọn là: A
PT
1
CM
3 tháng 7 2017
Phương trình dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
Đáp án cần chọn là: A
CM
6 tháng 4 2017
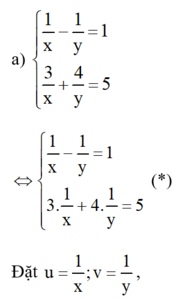
hệ phương trình (*) trở thành :
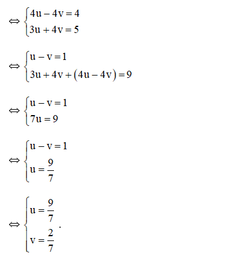
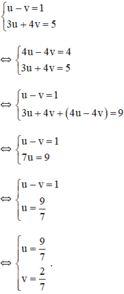
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
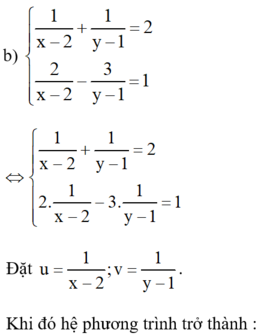
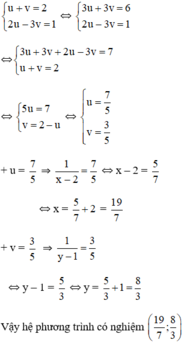
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
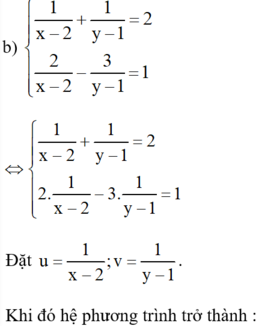
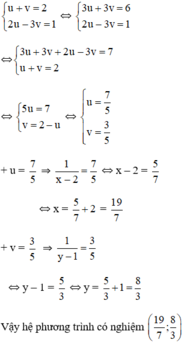
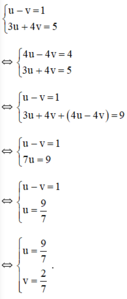
\(\frac{x+3}{5}\) = \(\frac{2x+1}{4}\)
4.(\(x+3\)) = 5.(2\(x\) + 1)
4\(x\) + 12 = 10\(x\) + 5
10\(x\) - 4\(x\) = 12 - 5
6\(x\) = 7
\(x=\frac76\)
Vậy \(x=\frac76\)