cho tam giác abc nhọn các dường cao bd,ce phân giác các góc abd và ace cắt nhau tại h cmr bhc=90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 4 2016
vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)
23 tháng 3 2016
mình làm được câu a, b, c rồi các bạn giúp mình câu d nhé thank
CM
6 tháng 10 2017
a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.
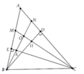
BH là phân giác của góc ABD
=>\(\hat{HBA}=\hat{HBD}=\frac12\cdot\hat{ABD}\)
CH là phân giác của góc ACE
=>\(\hat{ACH}=\hat{ECH}=\frac12\cdot\hat{ACE}\)
Ta có: \(\hat{HBC}+\hat{HCB}=\hat{HBD}+\hat{DBC}+\hat{HCE}+\hat{ECB}\)
\(=\frac12\cdot\hat{ABD}+\frac12\cdot\hat{ACE}+90^0-\hat{ACB}+90^0-\hat{ABC}\)
\(=\frac12\left(\hat{ABD}+\hat{ACE}\right)+180^0-\hat{ABC}-\hat{ACB}=\frac12\cdot2\cdot\hat{ABD}+\hat{BAC}=\hat{ABD}+\hat{BAD}=90^0\)
=>ΔBHC vuông tại H
=>\(\hat{BHC}=90^0\)