ho tgiac ABC vuông tại A ; M là trung điểm của BC . Vẽ MD vuông góc với AB tại D ; ME vuông góc với AC tại E . c/m a, vẽ AH vuông góc với BC . c/m tứ giác MHDE là hình thang cân b, qua A vẽ đường thẳng song2 với DH cắt DE tại K . c/m HK vuông góc với AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 giờ trước (9:44)
a: Ta có: MD⊥AB
AB⊥CA
Do đó: MD//AC
Ta có: ME⊥AC
AB⊥CA
Do đó: ME//AB
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\frac{BC}{2}\)
=>DE//MH
=>MHDE là hình thang
Xét tứ giác ADME có \(\hat{ADM}=\hat{AEM}=\hat{DAE}=90^0\)
nên ADME là hình chữ nhật
=>MD=AE và ME=AD
ΔHAC vuông tại H
mà HE là đường trung tuyến
nên EH=EA
=>EH=MD
Xét hình thang MHDE có MD=HE
nên MHDE là hình thang cân
b: Gọi I là giao điểm của DE và AH
ΔHAB vuông tại H
mà HD là đường trung tuyến
nên DA=DH
=>D nằm trên đường trung trực của AH(1)
EA=EH
=>E nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra DE là đường trung trực của AH
=>DE⊥AH tại I và I là trung điểm của AH
Xét ΔIAK vuông tại I và ΔIHD vuông tại I có
IA=IH
\(\hat{IAK}=\hat{IHD}\) (hai góc so le trong, AK//HD)
Do đó: ΔIAK=ΔIHD
=>IK=ID
=>I là trung điểm của KD
Xét tứ giác AKHD có
I là trung điểm chung của AH và KD
=>AKHD là hình bình hành
=>KH//AD
mà AD⊥CA
nên KH⊥AC
29 tháng 11 2021
1/ Xét tg vuông BEA và tg vuông BEM có
BE chung; \(\widehat{ABE}=\widehat{MBE}\Rightarrow\Delta BEA=\Delta BEM\) (Hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau)
2/
\(\Delta BEA=\Delta BEM\Rightarrow BA=BM\) => tg BAM cân tại B \(\Rightarrow BE\perp AM\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
3/ Xét tg vuông AEN và tg vuông MEC có
\(\Delta BEA=\Delta BEM\Rightarrow AE=ME\)
\(\widehat{AEN}=\widehat{MEC}\) (góc đối đỉnh)
\(\Rightarrow\Delta AEN=\Delta MEC\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) \(\Rightarrow AN=MC\)
4/ Ta có
BA=BM; AN=MC (cmt) => BA+AN=BM+MC => BN=BC => tg BNC cân tại B
Mà \(\widehat{ABE}=\widehat{MBE}\)
\(\Rightarrow BE\perp NC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Ta có \(BE\perp AM\left(cmt\right)\)
=> AM // NC (cùng vuông góc với BE)
18 tháng 12 2023
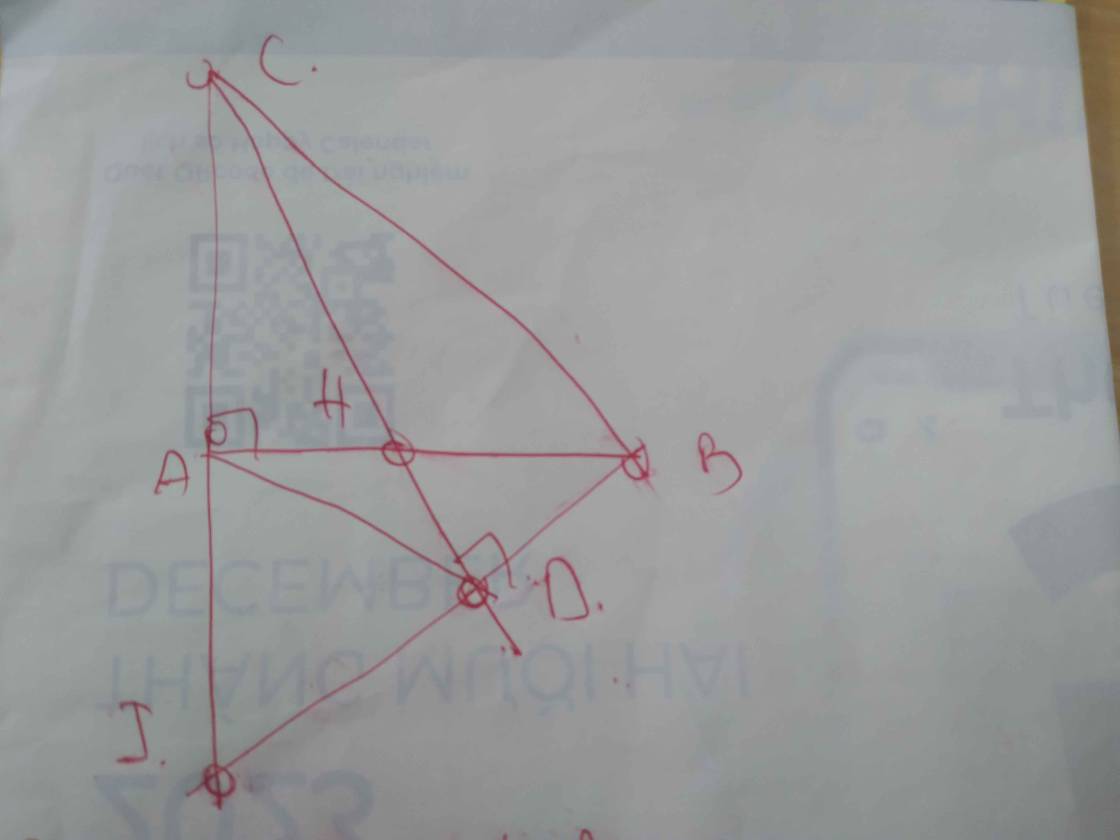
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
=>B nằm trên đường trung trực của AE(2)
Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm I của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC và AK=EC
Ta có: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của CK(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng
NP
1
19 tháng 8 2023
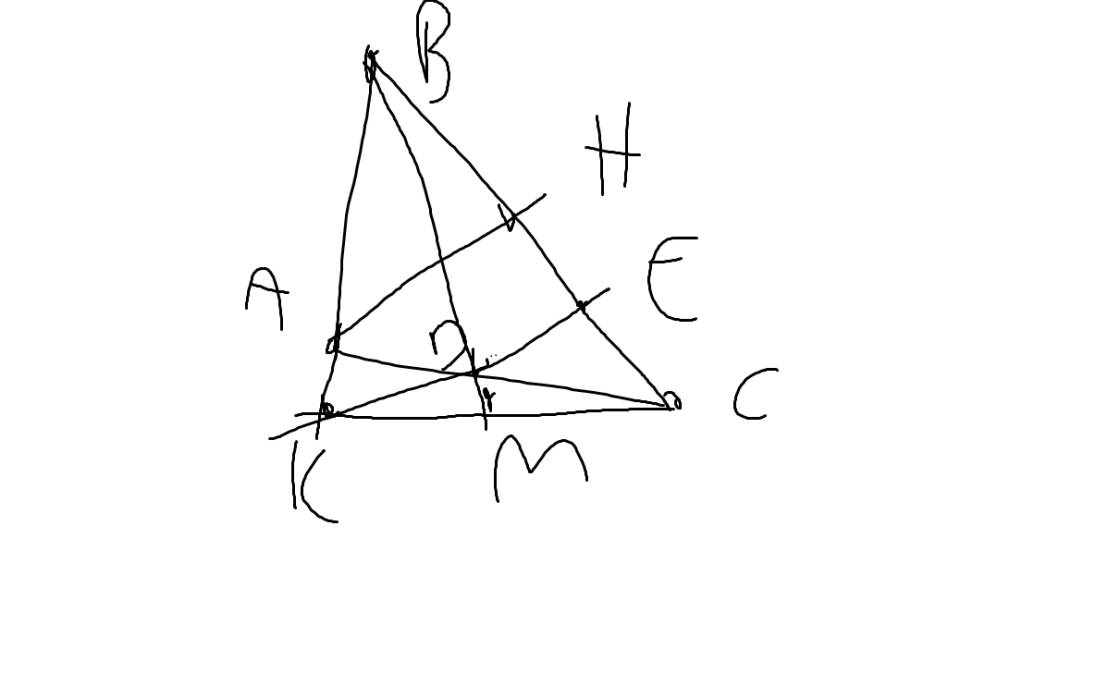
AH=căn AB^2-BH^2=3(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
=>BC=5^2/4=6,25(cm)
CH=6,25-4=2,25cm
AC=căn BC^2-AB^2=căn 6,25^2-5^2=3,75(cm)
a: Ta có: MD⊥AB
AB⊥CA
Do đó: MD//AC
Ta có: ME⊥AC
AB⊥CA
Do đó: ME//AB
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\frac{BC}{2}\)
=>DE//MH
=>MHDE là hình thang
Xét tứ giác ADME có \(\hat{ADM}=\hat{AEM}=\hat{DAE}=90^0\)
nên ADME là hình chữ nhật
=>MD=AE và ME=AD
ΔHAC vuông tại H
mà HE là đường trung tuyến
nên EH=EA
=>EH=MD
Xét hình thang MHDE có MD=HE
nên MHDE là hình thang cân
b: Gọi I là giao điểm của DE và AH
ΔHAB vuông tại H
mà HD là đường trung tuyến
nên DA=DH
=>D nằm trên đường trung trực của AH(1)
EA=EH
=>E nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra DE là đường trung trực của AH
=>DE⊥AH tại I và I là trung điểm của AH
Xét ΔIAK vuông tại I và ΔIHD vuông tại I có
IA=IH
\(\hat{IAK}=\hat{IHD}\) (hai góc so le trong, AK//HD)
Do đó: ΔIAK=ΔIHD
=>IK=ID
=>I là trung điểm của KD
Xét tứ giác AKHD có
I là trung điểm chung của AH và KD
=>AKHD là hình bình hành
=>KH//AD
mà AD⊥CA
nên KH⊥AC