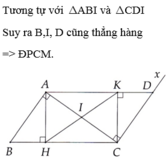
Cho đoạn thẳng AC có độ dài a. Trên đọan AC lấy điểm B sao cho AC=4AB. Tia Cx vuông góc với AC tại điểm C, gọi D là một điểm bất kỳ thuộc Cx. Từ điểm B kẻ đường thẳng vuông góc với AD cắt hai đường thẳng AD và CD lần lượt tại K, E
1) Xác định vị trí điểm D để tam giác BDE có diện tích nhỏ nhất
2) Chứng minh rằng khi điểm D thay đổi trên tia Cx thi đường tròn đường kính DE luôn có một dây cung cố định
Giúp em với ạ! Em cảm ơn trước ^^