Tìm nghiệm tổng quát của các phương trình sau:
a) 2x + 3y = -2
b) -2x + 5y = 0,5
c) x - y = -5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CT
1
CM
6 tháng 9 2019
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
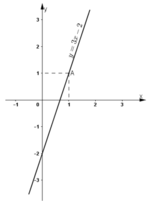
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
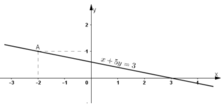
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y=3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ 
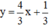
Vậy phương trình có nghiệm tổng quát là (x;4/3x+1/3)(x ∈ R).
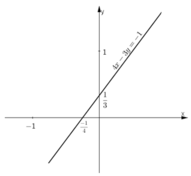
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0;1/3) .
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4;0) .
Vậy đường thẳng 4x – 3y = -1 đi qua (0;1/3) và (-1/4;0).
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔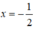 
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
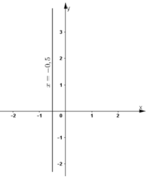
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
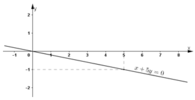
f) 0x + 2y = 5
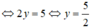
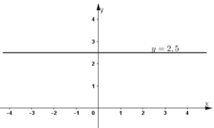
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
5 tháng 10 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}6x-9y=-15\\-6x+8y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-5\\-y=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-5+33}{2}=14\\y=11\end{matrix}\right.\)
5 tháng 10 2021
b: \(\left\{{}\begin{matrix}2x-3y=-5\\-3x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-9y=-15\\-6x+8y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=-11\\2x-3y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=11\\x=\dfrac{-5+3y}{2}=\dfrac{-5+3\cdot11}{2}=14\end{matrix}\right.\)
17 tháng 8 2021
a: Ta có: 2x-3y=9
nên 2x=9+3y
hay \(x=\dfrac{3y+9}{2}\)
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{3y+9}{2}\end{matrix}\right.\)
b: Ta có: 2x+0y=5
nên 2x=5
hay \(x=\dfrac{5}{2}\)
Vậy: \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y\in R\end{matrix}\right.\)
17 tháng 8 2021
a: Ta có: 2x-3y=9
nên 2x=9+3y
hay \(x=\dfrac{3y+9}{2}\)
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{3y+9}{2}\end{matrix}\right.\)
b: Ta có: 2x+0y=5
nên 2x=5
hay \(x=\dfrac{5}{2}\)
Vậy: \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y\in R\end{matrix}\right.\)
CM
12 tháng 9 2019
+ Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔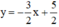 
Vậy phương trình (2) có nghiệm tổng quát là :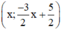 
(x ∈ R).
a)
Gọi \(y=t\left(t\in\Z\right)\)
Ta có:
\(2x+3t=-2\)
\(2x=-2-3t\)
\(x=\dfrac{-2-3t}{2}\in\Z\)
Đặt \(t=2k+0\left(k\in\Z\right)\rArr t\) chẵn mà \(3\) \(\cdot\) số chẵn \(=\) chẵn nên \(-2-3t\) là số chẵn và chia hết cho \(2\) \(\rArr x\in\Z\)
Do đó: \(\begin{cases}y=t=2k\\ x=\frac{-2-3\cdot2k}{2}=\frac{-2-6k}{2}=-1-3k\end{cases}\)
Vậy nghiệm tổng quát của phương trình là \(\begin{cases}y=2k\\ x=-1-3k\end{cases}\) với \(k\in\Z\)
b)
Gọi \(y=t\left(t\in\R\right)\)
Ta có:
\(-2x+5t=0,5\)
\(-2x=0,5-5t\)
\(x=\dfrac{5t-0,5}{2}\)
Vậy nghiệm tổng quát của phương trình là \(\begin{cases}y=t\\ x=\frac{5t-0,5}{2}\end{cases}\) với \(t\in\R\)
c)
Gọi \(y=t\left(t\in\R\right)\)
Ta có:
\(x-t=-5\)
\(x=-5+t\)
Vậy nghiệm tổng quát của phương trình là \(\begin{cases}y=t\\ x=-5+t\end{cases}\) với \(t\in\R\)