a^2 +b^2 +ab-5a-4b+2016
đưa về tổng bình và tìm giá trị nhở nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TM
1
Những câu hỏi liên quan
15 tháng 10 2016
Ta có \(2=a^2+b^2\ge2ab\)
\(\Leftrightarrow ab\le1\)
\(M\le\sqrt{\left(a^2+b^2\right)\left(36ab+45b^2+36ab+45a^2\right)}\)
\(=\sqrt{2\left(72ab+90\right)}\)\(\le\sqrt{2\left(72+90\right)}=\sqrt{324}=18\)
GTLN là 18 đạt được khi a = b = 1
ND
5
ND
0
NQ
0
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2022
\(A=\dfrac{x-4+5}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)+5}{\sqrt{x}-2}=\sqrt{x}+2+\dfrac{5}{\sqrt{x}-2}\)
\(=\sqrt{x}-2+\dfrac{5}{\sqrt{x}-2}+4\ge2\sqrt{\dfrac{5\left(\sqrt{x}-2\right)}{\sqrt{x}-2}}+4=4+2\sqrt{5}\)
\(A_{min}=4+2\sqrt{5}\) khi \(9+4\sqrt{5}\)
b.
Đặt \(\left(a;b;c\right)=\left(\dfrac{1}{x};\dfrac{1}{y};\dfrac{l}{z}\right)\Rightarrow xyz=1\)
\(B=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\ge\dfrac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(B_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\Rightarrow a=b=c=1\)
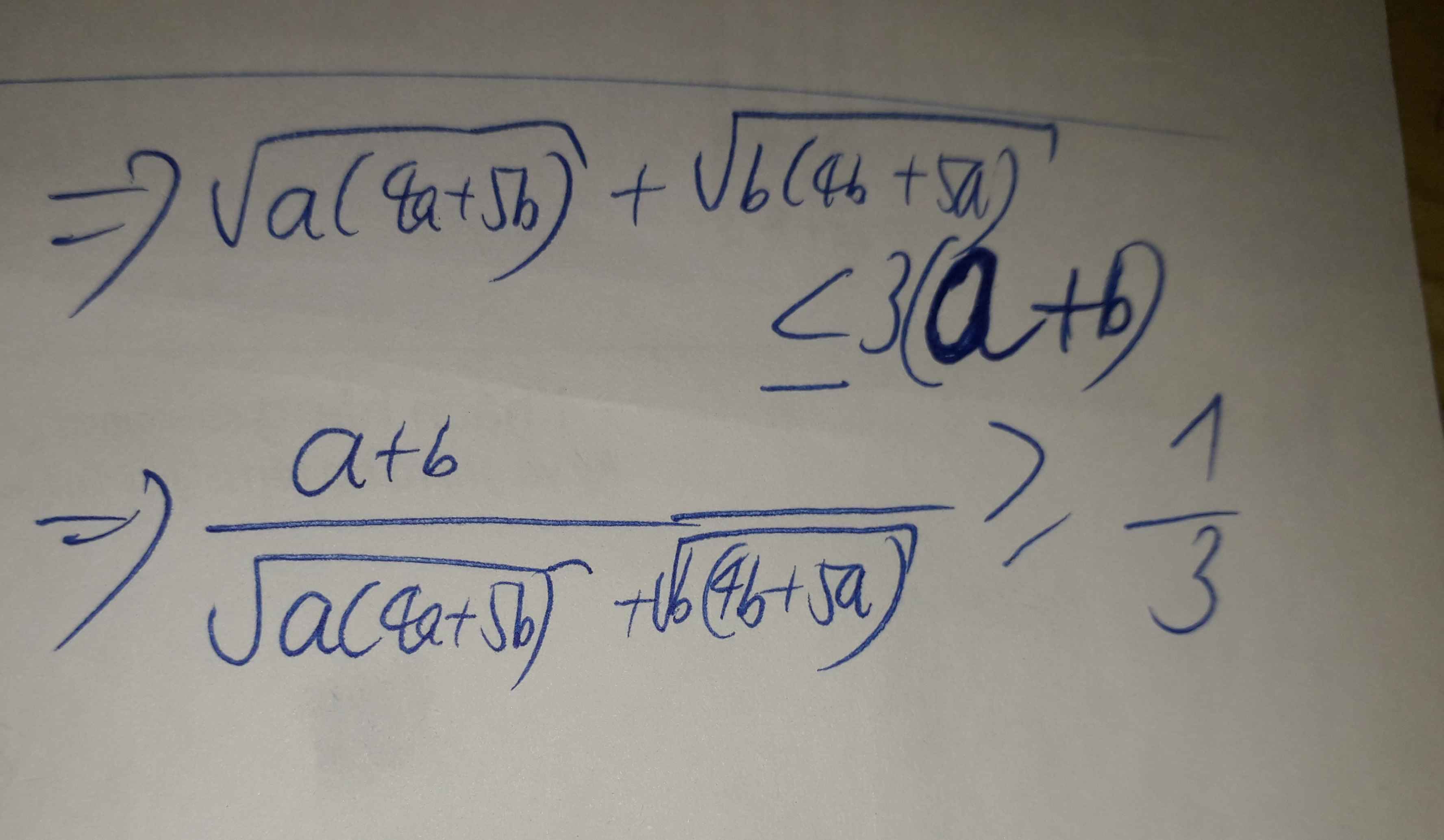
Đặt \(A = a^{2} + b^{2} + a b - 5 a - 4 b + 2016\)
Khi đó:
\(4 A = 4 a^{2} + 4 b^{2} + 4 a b - 20 a - 16 b + 8064\)
\(4 A = \left(\right. 4 a^{2} + b^{2} + 25 + 4 a b - 20 a - 10 b \left.\right) + \left(\right. 3 b^{2} - 6 b + 3 \left.\right) + 8036\)
\(4A=\left(2a+b-5\right)^2+3\left(b-1\right)^2+8036\)
Vì \(\left(2a+b-5\left.\right)\right.^2\geq0\) và \(\left(b-1\left.\right)\right.^2\geq0\) nên:
\(\left(2a+b-5\left.\right)\right.^2+3\left.\left(\right.b-1\right)^2\geq0\)
Suy ra:
\(4A=\left(2a+b-5\right)^2+3\left(\right.b-1\left.\right)^2+8036\geq8036\)
\(A \geq \frac{8036}{4} = 2009\)
Dấu "=" xảy ra khi và chỉ khi:
\({\begin{cases}2a+b-5=0\\ b-1=0\end{cases}}\)
\(\begin{cases}a=\frac{5 - b}{2}\\ b=1\end{cases}\)
\({\begin{cases}a=2\\ b=1\end{cases}}\)
Vậy giá trị nhỏ nhất của \(A = a^{2} + b^{2} + a b - 5 a - 4 b + 2016\) là \(2009\) tại \(a = 2\) và \(b = 1\)