Cho tam giác ABC cân tại A, kẻ đường cao AD. Trên AD lấy E là TĐ của AD. Kẻ DM vuông góc với BE ( M thuộc BE ).
CM: AM vuông góc với CM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
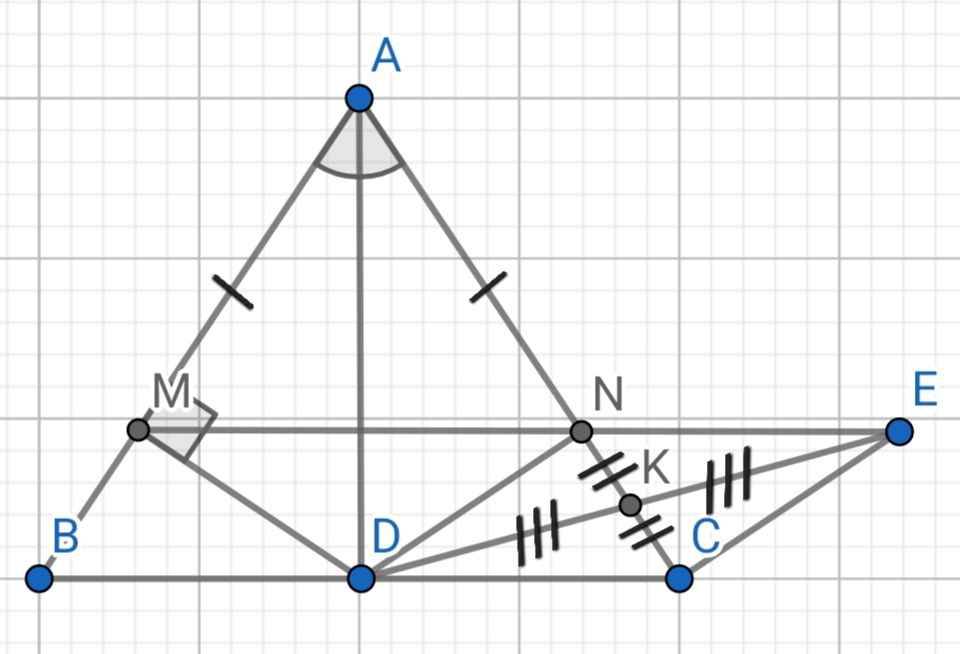
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

1, Do AD là đường cao của tam giác ABC cân tại A nên AD cũng đồng thời là trung tuyến của tam giác ABC
=> BD = DC
Mặt khác: gBDE = 180độ - gBED - gDBE = 90độ - gBED
gFDC = 180độ - gDFC - gFCD = 90độ - gFCD
Mà: gBED = gFCD(t/g ABC cân tại A) => gBDE = gFDC
Xét t/g EDB và t/g FDC có:
Góc EBD = Góc FCD(t/g ABC cân tại A); BD = DC(chứng minh trên); Góc BDE = Góc FDC(chứng minh trên)
=> t/g EDB = t/g FDC(g-c-g)
=> BE = CF(2 canhm tương ứng)
P/s: 'g' là viết tắt của góc. VD: gBDE là góc BDE
't/g' là viết tắt của tam giác
b) Hình như câu a) nhưng bạn cần nối thêm E lại với F và gọi giao của AD và EF là O(mình không vẽ lại nữa nha)
Do: t/g ABC cận tại A nên: gABC = gACB = (180độ - gBAC) : 2 (1) và AB = AC(2)
Mà: Theo câu a) thì BE = CF và từ (2) nên AB - BE = AC - CF hay AE = AF
=> t/g AEF cân tại A => gAEF = gAFE = (180độ - gBAC) : 2 (3)
Từ (1) và (3) ta được: gABC = gAEF => FE // BC(2 cặp đồng vị bằng nhau)
Mà: AD vuông góc với BC => AD vuông góc với EF (tại O) (*1)
Mặt khác: Ad là đường cao của t/g ABC cân tại A nen AD cũng là phân giác gBAC => gEAO = gFAO
Xét t/g AOE và t/g AOF có: AO chung; gEAO = gFAO(chứng minh trên); AE = AF(c/m trên)
=> t/g AOE = t/g AOF(c-g-c)
=> OE = OF(2 cạnh tương ứng) => O là trung điểm của EF mà O thuộc AD => AD đi qua trung điểm O của EF (*2)
Từ (*1) và (*2) ta được: AD là trung trực của EF

Hình tự vẽ
a ) Tam giác ABC cân tại A có đường cao AD => AD cũng là đường p/g
=> \(\widehat{BAD}=\widehat{CAD}\)
Do DE \(\perp\)AB => \(\widehat{DEA}=90^o\) => Tam giác AED vuông
Do DF \(\perp\)AC => \(\widehat{DFA}=90^o\) => Tam giác AFD vuông
Xét hai tam giác vuông : \(\Delta AED\)và \(\Delta AFD\)có :
AD là cạnh huyền chung
\(\widehat{BAD}=\widehat{CAD}\)( cmt )
nên tam giác AED = tam giác AFD ( cạnh huyền - góc nhọn )
=> AE = AF
Ta có :
AE + BE = AB
AF + CF = AC
mà AE = AF , AB = AC ( do tam giác ABC cân tại A )
=> BE = CF
b ) Gọi I là giao điểm của EF và AD
Xét \(\Delta AIE\)và \(\Delta AIF\)có :
AE = AF ( cm phần a )
\(\widehat{BAD}=\widehat{CAD}\)( cm phần a )
AI là cạnh chung
=> \(\Delta AIE=\Delta AIF\)( c.g.c )
=> IE = IF (1 )
và \(\widehat{AIE}=\widehat{AIF}\)
Ta có :
\(\widehat{AIE}+\widehat{AIF}=180^o\)( Hai góc kề bù )
\(\widehat{AIE}+\widehat{AIE}=180^o\)
\(\widehat{AIE}.2=180^o\)
\(\Rightarrow\widehat{AIE}=\frac{180^o}{2}=90^o\)
=> \(\widehat{AIE}=\widehat{AIF}=90^o\) ( 2 )
Từ ( 1 ) và ( 2 ) => AD là đường trung trực của EF
a) Vì ΔABCΔABC cân tại A => Bˆ=CˆB^=C^
mà AD là đường cao
=> AD là đường trung tuyến ΔABCΔABC
=> BD = DC
Xét ΔBEDΔBED và ΔCFDΔCFD có:
BEDˆ=CFDˆ(900)BED^=CFD^(900)
BD = DC (cmt)
Bˆ=Cˆ(cmt)B^=C^(cmt)
Do đó: ΔBED=ΔCFD(ch−gn)ΔBED=ΔCFD(ch−gn)
=> BE = CF (hai cạnh tương ứng)
b) Vì ΔBED=ΔCFD(cmt)ΔBED=ΔCFD(cmt)
=> ED = DF (hai cạnh tương ứng)
=> ΔEDFΔEDF cân tại D
=> D ∈∈ đường trung trực cạnh EF (1)
Xét ΔAEDΔAED và ΔAFDΔAFD có:
AD (chung)
AEDˆ=AFDˆ(=900)AED^=AFD^(=900)
ED = DF (cmt)
Do đó: ΔAED=ΔAFDΔAED=ΔAFD (cạnh huyền- cạnh góc vuông)
=> AE = AF(hai cạnh tương ứng)
=> ΔAEFΔAEF cân tại A
=> A ∈∈ đường trung trực cạnh EF (2)
(1); (2) => AD là đường trung trực cạnh EF
c) ta có: AD ⊥⊥ BC và AD⊥EFAD⊥EF
=> BC // EF
Gọi giao điểm của FM và DC là H ta có:
Xét ΔBEDΔBED và ΔCMDΔCMD có:
ED = DM (gt)
EDBˆ=CDMˆEDB^=CDM^ (đối đỉnh)
BD = DC (cmt)
Do đó: ΔBED=ΔCMDΔBED=ΔCMD (c-g-c)
mà ΔBED=ΔCFDΔBED=ΔCFD
=> ΔCMD=ΔCFDΔCMD=ΔCFD
=> CF = CM (hai cạnh tương ứng)
=> ΔFCMΔFCM cân tại C
=> C ∈∈đường trung trực cạnh FM (1)
DE = DF (cmt)
mà DE = DM
=> DF = DM
=> ΔFDMΔFDM cân tại D
=> D ∈∈ đường trung trực cạnh FM (2)
(1); (2) => DC là đường trung trực cạnh FM
=> DH ⊥⊥ FM
mà BC // EF
=> EF ⊥⊥ FH
=> EFMˆ=900EFM^=900 hay ΔEFMΔEFM vuông tại F
d) Vì ΔBED=ΔCMDΔBED=ΔCMD
=> BEDˆ=CMDˆ=900BED^=CMD^=900(hai góc tương ứng)
=> BE//CM(so le trong)
Gọi N, H lần lượt là trung điểm của BM và DM.
Xét tam giác ABC cân tại A ta có:
AD là đường cao (gt)
=> AD là đường trung tuyến của tam giác ABC
=> D trung điểm BC
Xét tam giác BMC ta có:
N trung điểm BM (cách vẽ)
D trung điểm BC (cmt)
=> ND là đường trung bình của tam giác BMC
=> ND // MC
Xét tam giác AMD ta có:
H trung điểm MD (cách vẽ)
E trung điểm AD (gt)
=> HE là đường trung bình của tam giác AMD
=> HE // AM
Xét tam giác BMD ta có:
N trung điểm MB (cách vẽ)
H trung điểm MD (cách vẽ)
=> NH là đường trung bình của tam giác BMD
=> NH // BD
Mà BD _|_ AD tại D (AD là đường cao của tam giác ABC)
Nên NH _|_ ED (E thuộc AD)
Xét tam giác BDE ta có:
DM là đường cao (DM _|_ BE tại M)
NH là đường cao (NH _|_ ED)
DM cắt NH tại H (gt)
=> H là trực tâm của tam giác BED
=> EH là đường cao thứ 3 của tam giác BED
=> EH _|_ ND
Mà ND // MC (cmt)
Nên EH _|_ MC
Mặt khác EH // AM (cmt)
=> AM _|_ MC tại M (đpcm)