Câu 7:.Tìm các số nguyên sao cho các phân số sau có giá trị là số nguyên:
a) 3/n-3 b)-5/2n-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2020
Để phân số :\(\frac{2n+3}{7}\) có giá trị là số nguyên thì 2n+3:7
\(\implies\) \(2n+3=7k\)
\(\implies\) 2n=7k-3
\(\implies\) n=\(\frac{7k-3}{2}\)
Vậy với mọi số nguyên n có dang \(\frac{7k-3}{2}\) thì phân số \(\frac{2n+3}{7}\) có giá trị là số nguyên
CM
14 tháng 12 2019
a) Để 3 n − 3 là số nguyên thì 3 chia hết cho (n - 3) hay (n-3) ÎƯ(3)
=> ( n – 3) Î{-3;-1;1;3} => n Î{-6;-4;-2;0}
b) ( n – 1) ÎƯ (3) = {-3;-1;1;3} => n Î{-2;0;2;4}
c) (3n +1) ÎƯ (4) {-4;-2;-1;1;2;4}
Vì n Î Z nên sau khi tính ta thu được nÎ{-1; 1}
JH
2 tháng 5 2022
Với n≠-2,n∈Z. Để 4/n+2 có giá trị là số nguyên thì 4⋮n+2
⇒n+2 ∈ Ư(4)={1;2;4;-1;-2;-4}
Nếu n+2=1⇒n=-1(TMĐK)
Nếu n+2=2⇒n=0(TMĐK)
Nếu n+2=4⇒n=2(TMĐK)
Nếu n+2=-1⇒n=-3(TMĐK)
Nếu n+2=-2⇒n=-4(TMĐK)
Nếu n+2=-4⇒n=-6(TMĐK)
Vậy với n ∈ {-1;0;2;-3;-4;-6} thì 4/n+2 có giá trị nguyên.
VD
16 tháng 3 2022
\(\dfrac{2n+5}{n-3}=\dfrac{\left(2n-6\right)+11}{n-3}=\dfrac{2\left(n-3\right)+11}{n-3}=2+\dfrac{11}{n-3}\)
Để biểu thức trên là số nguyên thì \(\dfrac{11}{n-3}\) nguyên\(\Rightarrow11⋮\left(n-3\right)\)\(\Rightarrow n-3\inƯ\left(11\right)\)
Ta có bảng:
| n-3 | -11 | -1 | 1 | 11 |
| n | -8 | 2 | 4 | 14 |
Vậy \(n\in\left\{-8;2;4;14\right\}\)
16 tháng 3 2022
\(\dfrac{2n+5}{n-3}=2+\dfrac{11}{n-3}\left(n\ne3\right).\)
Để \(\dfrac{2n+5}{n-3}\in Z.\Leftrightarrow n-3\inƯ\left(11\right)\) \(=\left\{1;-1;11;-11\right\}.\)
\(\Rightarrow n\in\left\{4;2;14;-8\right\}.\)
CM
15 tháng 9 2019
Để phân số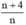 
có giá trị là số nguyên
thì n + 4 ⋮ n . Mà n ⋮ n
⇒ 4 ⋮ n ⇒ n ∈ Ư(4) = {±1; ±2; ±4}
Mặt khác, n là số tự nhiên ⇒ n ∈ {1; 2; 4}
CM
5 tháng 10 2018
Để phân số n n - 2 có giá trị là số nguyên
thì n ⋮ n - 2 ⇒ n - 2 + 2 ⋮ n - 2
Mà n - 2 ⋮ n - 2 ⇒ 2 ⋮ n - 2
⇒ (n – 2) ∈ Ư(2) = {±1; ±2}
Ta có bảng sau:
| n - 2 | -1 | 1 | -2 | 2 |
| n | 1 | 3 | 0 | 4 |
Kết hợp với điều kiện n là số tự nhiên
⇒ n ∈ {0; 1; 3; 4}
Vậy n ∈ {0; 1; 3; 4}.
CM
1 tháng 9 2019
Để phân số n - 2 4 có giá trị là số nguyên
thì n - 2 ⋮ 4 ⇒ n = 4k + 2 (k ∈ N)
CM
2 tháng 10 2017
Để phân số 6 n - 1 có giá trị là số nguyên
thì 6 ⋮ (n - 1)
⇒ (n – 1) ∈ Ư(6) = {±1; ±2; ±3; ±6}
Ta có bảng sau:
| n - 1 | -1 | 1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | 0 | 2 | 3 | -1 | 4 | -2 | 7 | -5 |
Kết hợp với điều kiện n là số tự nhiên
⇒ n ∈ {0; 2; 3; 4; 7}
Vậy n ∈ {0; 2; 3; 4; 7}.
Câu a:
Giải:
A = \(\frac{3}{n-3}\)(n ≠ 3)
A ∈ Z ⇔ 3 ⋮ (n -3)
(n - 3) ∈ Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
n - 3
-3
-1
1
3
n
0
2
4
6
Theo bảng trên ta có n ∈{0; 2; 4; 6}
Vậy n ∈ {0; 2; 4; 6}
Câu b:
B = \(\frac{-5}{2n-1}\)
B nguyên khi và chỉ khi 5 ⋮(2n - 1)
(2n -1) ∈ Ư(5) = {-5; -1; 1; 5}
Lập bảng ta có:
2n-1
-5
-1
1
5
n
-2
0
1
3
Theo bảng trên ta có: n ∈ {-2; 0; 1; 3}
Vậy n ∈ {-2; 0; 1; 3}