cho các số nguyên dương a b c d thỏa mãn ac=bd.Chứng minh M=a^2025+b^2025+c^2025+d^2025 là hợp số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9
Do x+y+z và |x|+|y|+|z| luôn cùng tính chẵn lẻ với mọi nguyên x,y,z
Suy ra \(\left|a-b\right|+\left|b-c\right|+\left|c-a\right|\) có cùng tính chẵn lẻ với a-b+b-c+c-a
Mà a-b+b-c+c-a=0 là số chẵn
Suy ra \(\left|a-b\right|+\left|b-c\right|+\left|c-a\right|\) chẵn
Do \(\left|a-b\right|+\left|b-c\right|+\left|c-a\right|=2024^{a}+2025^{a}\)
Nên \(2024^{a}+2025^{a}\) cũng là số chẵn
Nếu a≠0, do 2024 chẵn và 2025 lẻ nên \(2024^{a}+2025^{a}\) lẻ (ko thỏa mãn)
=>a=0
Thay vào đề bài:
\(\left|0-b\right|+\left|b-c\right|+\left|c-0\right|=2\Rightarrow\left|b\right|+\left|c\right|+\left|b-c\right|=2\)
- Nếu b,c đều khác 0, do b,c nguyên nên \(\left|b\right|\ge1;\left|c\right|\ge1\Rightarrow\left|b\right|+\left|c\right|\ge2\)
\(\Rightarrow\left|b\right|+\left|c\right|+\left|b-c\right|\ge2\)
Mà \(\left|b\right|+\left|c\right|+\left|b-c\right|=2\Rightarrow\begin{cases}\left|b\right|=1\\ \left|c\right|=1\\ \left|b-c\right|=0\end{cases}\) \(\Rightarrow b=c=\pm1\)
- Nếu trong 2 số b, có 1 số bằng 0. Do vai trò b,c như nhau, giả sử b=0
Thay vào: \(\left|0\right|+\left|c\right|+\left|0-c\right|=2\Rightarrow2\left|c\right|=2\Rightarrow\left|c\right|=1\)
\(\Rightarrow c=\pm1\)
Vậy các sộ số nguyên a,b,c thỏa mãn yêu cầu là:
\(\left(a,b,c\right)=\left(0,0,1\right);\left(0,1,0\right),\left(0,0,-1\right),\left(0,-1,0\right);\left(0,1,1\right),\left(0,-1,-1\right)\)
TH
Trần Hoàng Trung
VIP
3 tháng 9
Cho bài toán:
Tìm các số nguyên \(a , b , c\) sao cho:
\(\mid a - b \mid + \mid b - c \mid + \mid c - a \mid = 2024^{a} + 2025^{a}\)
Phân tích:
- Vế trái là tổng ba giá trị tuyệt đối, luôn không âm.
- Vế phải là tổng hai số mũ với cơ số lớn \(2024\) và \(2025\), lũy thừa \(a\).
- \(a , b , c \in \mathbb{Z}\) (số nguyên).
Bước 1: Bất đẳng thức về tổng các giá trị tuyệt đối
Ta có:
\(\mid a - b \mid + \mid b - c \mid \geq \mid a - c \mid\)
Do đó:
\(\mid a - b \mid + \mid b - c \mid + \mid c - a \mid \geq \mid a - c \mid + \mid c - a \mid = 2 \mid a - c \mid\)
Nhưng bên trái thực ra bằng:
\(\mid a - b \mid + \mid b - c \mid + \mid c - a \mid = 2 \times (\text{kho}ả\text{ng}\&\text{nbsp};\text{c} \overset{ˊ}{\text{a}} \text{ch}\&\text{nbsp};\text{l}ớ\text{n}\&\text{nbsp};\text{nh} \overset{ˊ}{\hat{\text{a}}} \text{t}\&\text{nbsp};\text{gi}ữ\text{a}\&\text{nbsp};\text{c} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{s} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp}; a , b , c )\)
Cụ thể, vì tổng ba giá trị tuyệt đối của 3 điểm trên trục số là gấp đôi độ dài đoạn thẳng lớn nhất giữa chúng.
Bước 2: Xét vế phải
- Nếu \(a < 0\), thì \(2024^{a}\) và \(2025^{a}\) là các số phân số rất nhỏ (dương) do số mũ âm.
- Nếu \(a = 0\), thì:
\(2024^{0} + 2025^{0} = 1 + 1 = 2\)
- Nếu \(a > 0\), thì \(2024^{a} + 2025^{a}\) là số rất lớn, nhanh tăng.
Bước 3: So sánh quy mô hai vế
- Vế trái là số nguyên không âm, ít nhất là 0.
- Vế phải là số dương (do lũy thừa dương), rất lớn nếu \(a > 0\).
Bước 4: Xét từng trường hợp
- Trường hợp \(a < 0\):
Vế phải là số nhỏ hơn 2 (do \(2024^{a} , 2025^{a} < 1\)), còn vế trái là số nguyên không âm (phải là số nguyên, vì \(a , b , c\) nguyên), nên vế trái ít nhất bằng 0. Rất khó bằng một số phân số nhỏ.
- Trường hợp \(a = 0\):
Vế phải là \(2\).
Vậy:
\(\mid a - b \mid + \mid b - c \mid + \mid c - a \mid = 2\)
Vì \(a = 0\), thì \(a = 0\).
Ta cần tìm \(b , c\) nguyên sao cho:
\(\mid 0 - b \mid + \mid b - c \mid + \mid c - 0 \mid = 2\)
Cách này ta dễ kiểm tra.
- Gọi \(b = m\), \(c = n\).
Ta có:
\(\mid m \mid + \mid m - n \mid + \mid n \mid = 2\)
Bước 5: Tìm \(m , n\) nguyên thỏa mãn
Ta cần tổng ba giá trị tuyệt đối bằng 2.
- Các giá trị tuyệt đối là không âm, nên tổng ba số này bằng 2 nghĩa là tổng này khá nhỏ.
Thử các trường hợp:
- Nếu \(m = 0\), thì
\(0 + \mid 0 - n \mid + \mid n \mid = \mid n \mid + \mid n \mid = 2 \mid n \mid = 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \mid n \mid = 1\)
- Nếu \(m = 0 , n = \pm 1\) thì tổng đúng bằng 2.
- Nếu \(n = 0\), thì
\(\mid m \mid + \mid m - 0 \mid + 0 = \mid m \mid + \mid m \mid = 2 \mid m \mid = 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \mid m \mid = 1\)
- Nếu \(m = \pm 1 , n = 0\), cũng thỏa.
- Nếu \(m = n\), thì
\(\mid m \mid + 0 + \mid m \mid = 2 \mid m \mid = 2 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } \mid m \mid = 1\)
Thí dụ: \(m = n = \pm 1\)
Bước 6: Tổng hợp nghiệm
Với \(a = 0\), \(b , c\) thỏa mãn:
\(\mid b \mid + \mid b - c \mid + \mid c \mid = 2\)
Các bộ nghiệm là:
- \(\left(\right. b , c \left.\right) = \left(\right. 0 , \pm 1 \left.\right) , \left(\right. \pm 1 , 0 \left.\right) , \left(\right. \pm 1 , \pm 1 \left.\right)\)
Bước 7: Trường hợp \(a > 0\)
Vế phải rất lớn, vế trái nhỏ nhất là 0 (khi \(a = b = c\)), nhưng không thể bằng một số rất lớn. Do đó, không thỏa.
Kết luận:
- Các số nguyên \(a , b , c\) thỏa mãn phương trình là:
\(a = 0\)
và
\(\mid b \mid + \mid b - c \mid + \mid c \mid = 2\)
Cụ thể các bộ \(\left(\right. b , c \left.\right)\) như trên.
25 tháng 8 2019
105 - 105 = 0 (Không là hợp số cũng không phải số nguyên)
210 - 207 = 3 (Số nguyên)
144 - 142 = 2 (Số nguyên)
Phép này có + và . thôi mà đâu có trừ đâu?
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2024
\(4\left(a+b+c\right)=a^2+\left(b+c\right)^2\ge\dfrac{1}{2}\left(a+b+c\right)^2\)
\(\Rightarrow a+b+c\le8\)
\(a^2+16-16\ge8a-16\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{8100}{\sqrt{2a+2b+1}+\sqrt{2c+1}}\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{48600}{6\sqrt{2a+2b+1}+6\sqrt{2c+1}}\)
\(\Rightarrow P\ge8\left(a+b+c\right)-16+\dfrac{24300}{a+b+c+10}\)
\(\Rightarrow P\ge8\left(a+b+c+10+\dfrac{324}{a+b+c+10}\right)+\dfrac{21708}{a+b+c+10}-96\)
\(\Rightarrow P\ge16.\sqrt{324}+\dfrac{21708}{18}-96=1398\)
Dấu "=" xảy ra tại \(\left(a;b;c\right)=\left(4;0;4\right)\)
26 tháng 7 2021
Đặt \(\overline{ab}=x;\overline{cd}=y\Rightarrow\overline{abcd}=100\overline{ab}+\overline{cd}\)
\(=100x+y\left(10\le x\le99;y\ge0\right)\)
\(\Rightarrow100x+y=\left(x+y\right)^2\)
\(=x^2+2xy+y^2\left(1\right)\)
\(\Rightarrow x^2+\left(2y-100\right)x+\left(y^2-y\right)=0\left(2\right)\)
Để \(x,y\inℤ\)thoản mãn (1) \(\Rightarrow\left(2\right)\)có nghiệm nguyên
\(\Rightarrow\Delta'=\left(y-50\right)^2-\left(y^2-y\right)\)
\(=y^2-100y+2500-y^2+y\)
\(=-99y+2500\)
\(\Rightarrow\Delta'\ge0\Leftrightarrow2500-99y\ge0\)
\(\Rightarrow y\le25\)
(1) có nghiệm nguyên khi \(\sqrt{\Delta'}\)là số nguyên
\(\Rightarrow y\in\left\{0;1;25\right\}\)
\(\cdot y=0\Rightarrow\sqrt{\Delta'}=50\Rightarrow\orbr{\begin{cases}x_1=\left(50-y\right)+\sqrt{\Delta'}=50+50=100\\x_2=\left(50-y\right)-\sqrt{\Delta'}=50-50=0\end{cases}\left(loại\right)}\)
tính tương tự với y=1 ; y =25 nha cậu
CM
8 tháng 9 2018
a) X = {2012 ; 2016 ; 2020 ; 2024}
b)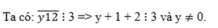
y + 3 ⋮ 3 => y ⋮ 3
Mà: y ∈ {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6} và y ≠ 0 nên y ∈ {3 ; 6}.
Vậy số cần tìm là 312 ; 612.
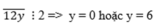
Vậy số cần tìm là 120 ; 126.
Vì ab cd = nên 2025 2025 2025 2025 ab cd = Ta có 2025 2025 2025 2025 Ma b c d = +++ suy ra 2025 2025 2025 2025 2025 2025 a Ma a b c d . .( = +++ ) 0,5 hay 2025 2025 2025 2025 2025 2025 2025 2025 2025 a Ma a a b a c a d .. . . . = + ++ 2025 2025 2025 2025 2025 2025 2025 2025 2025 a Ma a a c c d a d .. . . . = ++ + 0,5 2025 2025 2025 2025 2025 2025 2025 a Ma a c d c a . .( ) .( ) = ++ + 2025 2025 2025 2025 2025 aMa d a c . ( ).( ) =+ + 0,5 Giả sử M là số nguyên tố suy ra 2025 2025 acM + (vô lý) hoặc 2025 2025 adM + (vô lý) nên M là hợp số.