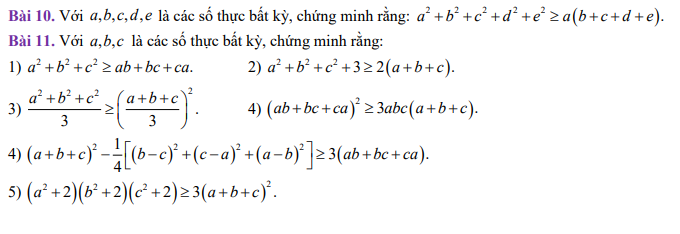giúp em làm ạ!! làm được bài nào thì cứ gửi thôi. Khó quá!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LM
0
Những câu hỏi liên quan
CB
1
17 tháng 12 2023
a: |x|=5,6
=>\(\left[{}\begin{matrix}x=5,6\\x=-5,6\end{matrix}\right.\)
c: \(\left|x\right|=3\dfrac{1}{5}\)
=>\(\left|x\right|=3,2\)
=>\(\left[{}\begin{matrix}x=3,2\\x=-3,2\end{matrix}\right.\)
d: |x|=-2,1
mà -2,1<0
nên \(x\in\varnothing\)
d: |x-3,5|=5
=>\(\left[{}\begin{matrix}x-3,5=5\\x-3,5=-5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8,5\\x=-1,5\end{matrix}\right.\)
e: \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
=>\(\left|x+\dfrac{3}{4}\right|=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{2}\\x+\dfrac{3}{4}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
f: \(\left|4x\right|-\left|-13,5\right|=\left|2\dfrac{1}{4}\right|\)
=>\(4\left|x\right|=2,25+13,5=15,75\)
=>\(\left|x\right|=\dfrac{63}{16}\)
=>\(x=\pm\dfrac{63}{16}\)
g: \(\dfrac{5}{6}-\left|2-x\right|=\dfrac{1}{3}\)
=>\(\dfrac{5}{6}-\left|x-2\right|=\dfrac{1}{3}\)
=>\(\left|x-2\right|=\dfrac{5}{6}-\dfrac{1}{3}=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x-2=\dfrac{1}{2}\\x-2=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\)
h: \(\left|x-\dfrac{2}{5}\right|+\dfrac{1}{2}=\dfrac{3}{4}\)
=>\(\left|x-\dfrac{2}{5}\right|=\dfrac{3}{4}-\dfrac{1}{2}=\dfrac{1}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{2}{5}=\dfrac{1}{4}\\x-\dfrac{2}{5}=-\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}+\dfrac{2}{5}=\dfrac{13}{20}\\x=-\dfrac{1}{4}+\dfrac{2}{5}=\dfrac{-5+8}{20}=\dfrac{3}{20}\end{matrix}\right.\)
i: \(\left|5-3x\right|+\dfrac{2}{3}=\dfrac{1}{6}\)
=>\(\left|3x-5\right|=\dfrac{1}{6}-\dfrac{2}{3}=\dfrac{1}{6}-\dfrac{4}{6}=-\dfrac{3}{6}=-\dfrac{1}{2}< 0\)
=>\(x\in\varnothing\)
k: \(-2,5+\left|3x+5\right|=-1,5\)
=>|3x+5|=-1,5+2,5=1
=>\(\left[{}\begin{matrix}3x+5=1\\3x+5=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-4\\3x=-6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=-2\end{matrix}\right.\)
m: \(\dfrac{1}{5}-\left|\dfrac{1}{5}-x\right|=\dfrac{1}{5}\)
=>\(\left|\dfrac{1}{5}-x\right|=\dfrac{1}{5}-\dfrac{1}{5}=0\)
=>\(\dfrac{1}{5}-x=0\)
=>\(x=\dfrac{1}{5}\)
n: \(-\dfrac{22}{15}x+\dfrac{1}{3}=\left|-\dfrac{2}{3}+\dfrac{1}{5}\right|\)
=>\(-\dfrac{22}{15}x+\dfrac{1}{3}=\dfrac{2}{3}-\dfrac{1}{5}\)
=>\(-\dfrac{22}{15}x=\dfrac{1}{3}-\dfrac{1}{5}=\dfrac{2}{15}\)
=>-22x=2
=>\(x=-\dfrac{1}{11}\)
DV
2 tháng 12 2016
x : 3 dư 2
x : 5 dư 1
→ x + 4 chia hết cho 3 và 5
→ x + 4 € BC ( 3, 5 )
Ta có: 3 . 5 = 15
→ BC ( 3, 5 ) = B ( 15 ) = {0;15;30;45;...}
Dựa vào các điều kiện trên, ta kết luận: Vậy x € { 15;30 }
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
BB
0
TA
3
23 tháng 9 2021
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
23 tháng 9 2021
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
BP
1
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
25 tháng 10 2021
Bài 4:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
hay ΔOAB cân tại O