Giải Phương trình
x4+2x3+2x2+2x+1=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^4+2x^3-2x^2+2x-3=0\\ \Leftrightarrow x^4+3x^3-x^3-3x^2+x^2+3x-x-3=0\\ \Leftrightarrow x^3\left(x+3\right)-x^2\left(x+3\right)+x\left(x+3\right)-\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x^3-x^2+x-1\right)=0\\ \Leftrightarrow\left(x+3\right)\left[x^2\left(x-1\right)+\left(x-1\right)\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\\x^2+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\left(\text{vì }x^2+1\ge1>0\right)\)
Vậy ...
\(\left(x-1\right)\left(x^2+5x-2\right)-x^3+1=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+5x-2\right)-\left(x^3-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^2+5x-2\right)-\left(x-1\right)\left(x^2+x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left[\left(x^2+5x-2\right)-\left(x^2+x+1\right)\right]=0\\ \Leftrightarrow\left(x-1\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy ...
\(x^2+\left(x+2\right)\left(11x-7\right)=4\\ \Leftrightarrow x^2-4+\left(x+2\right)\left(11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x-2\right)+\left(11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x-2+11x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(12x-9\right)=0\\ \Leftrightarrow3\left(x+2\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+2=0\\4x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy ...
nghiệm đâu bạn ưi...nó là phương trình vô nghiệm hay vô số nghiệm vậy m :))

2(x2 – 2x)2 + 3(x2 – 2x) + 1 = 0 (1)
Đặt x2 – 2x = t,
(1) trở thành : 2t2 + 3t + 1 = 0 (2).
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = -1/2.
+ Với t = -1 ⇒ x2 – 2x = -1 ⇔ x2 – 2x + 1 = 0 ⇔ (x – 1)2 = 0 ⇔ x = 1.
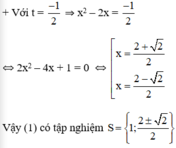

Ta có:
2x2 + 5 ≤ 2x – 1
⇔ 2x2 + 5 + 1 – 2x ≤ 2x – 1 + 1 – 2x (Cộng cả hai vế của BPT với 1 – 2x).
⇔ 2x2 – 2x + 6 ≤ 0.
Vậy hai BPT đã cho tương đương: 2x2 + 5 ≤ 2x – 1 ⇔ 2x2 – 2x + 6 ≤ 0.

a: Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x-1\right)^3\cdot\left(x+1\right)\)
b: Ta có: \(-a^4+a^3+2a^3+2a^2\)
\(=-a^2\left(a^2-a-2a-2\right)\)
c: Ta có: \(x^4+x^3+2x^2+x+1\)
\(=x^4+x^3+x^2+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^2+1\right)\)

\(a,=\left(2x^3-x^2+x+4x^2-2x+2-x+1\right):\left(2x^2-x+1\right)\\ =\left[x\left(2x^2-x+1\right)+2\left(2x^2-x+1\right)-x+1\right]:\left(2x^2-x+1\right)\\ =x+2\left(\text{dư }-x+1\right)\\ b,=\left[x^2\left(2x-5\right)+3\left(2x-5\right)\right]:\left(2x-5\right)\\ =x^2+3\)

a) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 ( 1 )
Đặt x 2 – 2 x = t ,
(1) trở thành : 2 t 2 + 3 t + 1 = 0 ( 2 ) .
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = - 1 / 2 .
+ Với t = -1 ⇒ x 2 − 2 x = − 1 ⇔ x 2 − 2 x + 1 = 0 ⇔ ( x − 1 ) 2 = 0 ⇔ x = 1
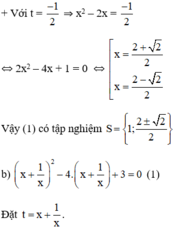
(1) trở thành: t 2 – 4 t + 3 = 0 ( 2 )
Giải (2):
Có a = 1; b = -4; c = 3
⇒ a + b + c = 0
⇒ (2) có nghiệm t 1 = 1 ; t 2 = c / a = 3 .
+ t = 1 ⇒ x + 1/x = 1 ⇔ x 2 + 1 = x ⇔ x 2 – x + 1 = 0
Có a = 1; b = -1; c = 1 ⇒ Δ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
Phương trình vô nghiệm.


a) 2x. (x2 – 7x -3)
= 2x3- 14x2- 6x
b) ( -2x3 + y2 -7xy). 4xy2
= -8x4y2+ 4xy4- 28x2y3
c)(-5x3).(2x2+3x-5)
= -10x5-15x4+25x3
d) (2x2 - xy+ y2).(-3x3)
=-6x5+ 3x4y -3x3y2
e)(x2 -2x+3). (x-4)
=x3-2x2+3x -4x2+8x-12
=x3-6x2+11x-12
f) ( 2x3 -3x -1). (5x+2)
=10x4-15x2-5x +4x3-6x-2
=10x4+4x3-15x2-11x-2

(2x2 + x – 4)2 – (2x – 1)2 = 0
⇔ (2x2 + x – 4 – 2x + 1)(2x2 + x – 4 + 2x – 1) = 0
⇔ (2x2 – x – 3)(2x2 + 3x – 5) = 0
⇔ 2x2 – x – 3 = 0 (1)
hoặc 2x2 + 3x – 5 = 0 (2)
+ Giải (1): 2x2 – x – 3 = 0
Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.
+ Giải (2): 2x2 + 3x – 5 = 0
Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.
Vậy phương trình có tập nghiệm 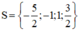

a: \(=6x^3-10x^2+6x\)
b: \(=-2x^4-10x^3+6x^2\)
c: \(=-x^5+2x^3-\dfrac{3}{2}x^2\)
d: \(=2x^3+10x^2-8x-x^2-5x+4=2x^3+9x^2-13x+4\)
\(^{x^4+2x^3+2x^2+2x+1=\left(x^4+2x^2+1\right)+\left(2x^3+2x\right)=\left(x^2+1\right)+2x\left(x^2+1\right)=\left(x^2+1\right)\left(x^2+2x+1\right)=\left(x^2+1\right)\left(x+1\right)^2}\)
Vì \(\left(x^2+1\right)\)>0 => \(\left(x+1\right)^2\)=0 hay \(x=-1\)