Tạo chương trình vẽ hình vuông với một đường chéo.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
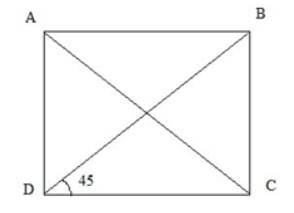
Góc tạo bởi một đường chéo và một cạnh hình vuông bằng 45 độ.
13 tháng 9 2023
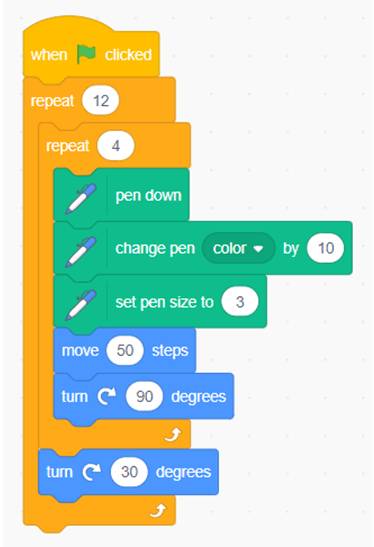
- Sử dụng vòng lặp với số lần lặp là 12
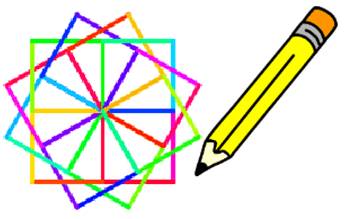
Kết quả thu được là
9 tháng 3 2023
#include <bits/stdc++.h>
using namespace std;
int main()
{
double a;
cin>>a;
cout<<a*4<<endl;
cout<<a*a<<endl;
cout<<a*sqrt(2)<<endl;
return 0;
}
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Các đường thẳng nối mỗi điểm A, B, C với bóng A', B', C' có đôi một song song.
b) Để xác định được bóng đổ trên sàn nhà của mỗi điểm trên khung cửa sổ ta lấy một đường thẳng a cố định song song với ánh mặt trời.
Điểm O' là giao điểm của sàn nhà và đường thẳng đi qua O song song với a.
Tương tự, ta xác định được các điểm A', B', C', D'.
CM
11 tháng 10 2018
a)
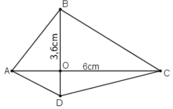
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.
Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD.
Diện tích tứ giác ABCD là:
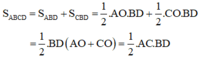
Mà AC = 6cm ; BD = 3,6 cm nên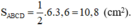 
b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: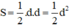 
NN
NL
21 tháng 4 2017
a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác ABCD ở hình dưới có
AC = 6cm
BD = 3,6cm
AC ⊥⊥ BD
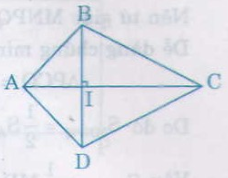
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:
AC = 6cm
BD = 3,6cm
AC ⊥⊥ BD tại I với I là điểm tùy ý thuộc đoạn AC và BD
Diện tích củ tứ giác vừa vẽ:
SABCD = 1212 AC. BD = 1212 6. 3,6 = 10,8 (cm2)
b) Diện tích hình vuông có độ dài đường chéo là d
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
S = 1212 d.d = 1212 d2
21 tháng 4 2017
tứ giác ABCD ở hình dưới có
AC = 6cm
BD = 3,6cm
AC ⊥⊥ BD
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:
AC = 6cm
BD = 3,6cm
AC ⊥⊥ BD tại I với I là điểm tùy ý thuộc đoạn AC và BD
Diện tích củ tứ giác vừa vẽ:
SABCD = 1212 AC. BD = 1212 6. 3,6 = 10,8 (cm2)
b) Diện tích hình vuông có độ dài đường chéo là d
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
S = 1212 d.d = 1212 d2