Cho tam giác ABC và O là điểm nằm trong tam giác đó. Gọi M, N, K lần lượt là giao điểm của AO với BC, BO với AC và CO với AB. Qua O, kẻ các đoạn thẳng EF, PQ, IJ sao cho EF//BC (E thuộc AB, F thuộc ![]() AC), PQ//AC (P thuộc AB, Q thuộc BC)
AC), PQ//AC (P thuộc AB, Q thuộc BC)![]() , IJ//AB (I thuộc AC, J thuộc BC
, IJ//AB (I thuộc AC, J thuộc BC![]() ).
).
1) Chứng minh ![]() \(\frac{OM}{AM}+\frac{ON}{BN}+\frac{OK}{CK}=1\)
\(\frac{OM}{AM}+\frac{ON}{BN}+\frac{OK}{CK}=1\)
2) Chứng minh ![]() .\(\frac{EF}{BC}+\frac{PQ}{AC}+\frac{IJ}{AC}=2\)
.\(\frac{EF}{BC}+\frac{PQ}{AC}+\frac{IJ}{AC}=2\)

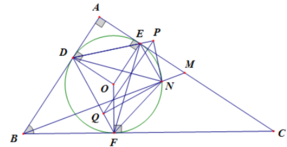


a) Xét \(\Delta\)AMC: OQ//AC (O\(\in\)AM; Q\(\in\)MC) => \(\frac{OM}{AM}=\frac{MQ}{MC}\)(1)
Tương tự, ta có: \(\frac{OM}{AM}=\frac{MJ}{BM}\)(2)
Từ (1) và (2) => \(\frac{OM}{AM}=\frac{MQ+MJ}{BM+MC}=\frac{JQ}{BC}\)(Tính chất dãy tỉ số bằng nhau)
Xét \(\Delta\)BNC: OQ//NC (O\(\in\)BN; Q\(\in\)BC) => \(\frac{ON}{BN}=\frac{QC}{BC}\)
Tương tự: \(\frac{OK}{CK}=\frac{BJ}{BC}\)
Vây \(\frac{OM}{AM}+\frac{ON}{BN}+\frac{OK}{CK}=\frac{JQ}{BC}+\frac{QC}{BC}+\frac{BJ}{BC}=\frac{BC}{BC}=1\)(đpcm).
b) Đề sai thì phải, theo mình nên sửa \(\frac{IJ}{AC}\)thành \(\frac{IJ}{AB}\)
Ta có: \(\frac{PQ}{AC}=\frac{BQ}{BC}\) và \(\frac{IJ}{AB}=\frac{CJ}{BC}\)(Hệ quả ĐL Thales)
\(\frac{EF}{BC}=\frac{OE}{BC}+\frac{OF}{BC}\)
Lại có: \(\frac{OE}{BC}=\frac{OK}{KC}=\frac{BJ}{BC}\); \(\frac{OF}{BC}=\frac{ON}{BN}=\frac{QC}{BC}\)
\(\Rightarrow\frac{EF}{BC}=\frac{BJ+QC}{BC}\)
\(\Rightarrow\frac{EF}{BC}+\frac{PQ}{AC}+\frac{IJ}{AB}=\frac{BJ+QC+BQ+CJ}{BC}=\frac{BJ+JQ+CJ+JQ+BJ+CJ}{BC}\)
\(=\frac{2BJ+2JQ+2CJ}{BC}=\frac{2.\left(BJ+JQ+CJ\right)}{BC}=\frac{2BC}{BC}=2\)
Vậy: \(\frac{EF}{BC}+\frac{PQ}{AC}+\frac{IJ}{AB}=2\)(đpcm).