Cho ΔABCΔABCcó AB=AC. Gọi M là trung điểm của BCa) Chứng minh rằng ΔABM=ΔACMΔABM=ΔACMb)Từ M kẻ MH⊥⊥Ac tại H. Trên tia đối của tia HM lấy điểm D sao cho H là trung điểm của MD. Chứng minh rằng CA là tia phân giác của ˆMCDMCD^c)Đường thẳng qua H và song song vs AD cắt CD tại E. Chứng minh rằng HE⊥CDHelp nha ^_^. mik sắp đi hok rồi, chỉ cần í cuối cx đc, hai í đầu mik tự...
Đọc tiếp
Cho ΔABCΔABCcó AB=AC. Gọi M là trung điểm của BC
a) Chứng minh rằng ΔABM=ΔACMΔABM=ΔACM
b)Từ M kẻ MH⊥⊥Ac tại H. Trên tia đối của tia HM lấy điểm D sao cho H là trung điểm của MD. Chứng minh rằng CA là tia phân giác của ˆMCDMCD^
c)Đường thẳng qua H và song song vs AD cắt CD tại E. Chứng minh rằng HE⊥CD
Help nha ^_^. mik sắp đi hok rồi, chỉ cần í cuối cx đc, hai í đầu mik tự lm đc
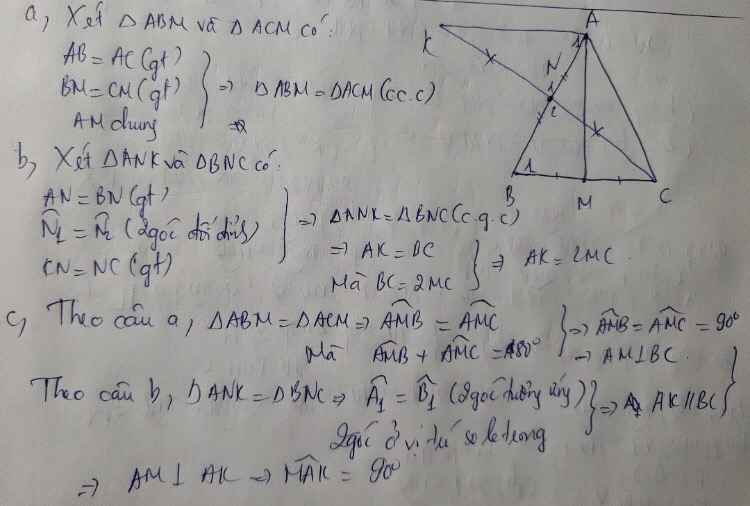
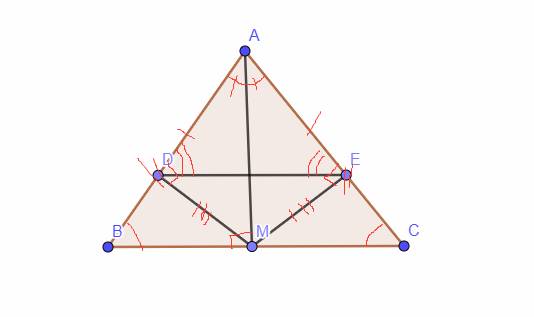
c. Theo câu a, tam giác ABM= tam giác ACM (ccc) => AMB=AMC
Mà AMB+AMC=180*(kề bù)
=> AMB=90*
Xét tam giác HCM và tam giác HCD
MH=DH
MHC=DHC=90*
HC chung
=> tam giác HCM= tam giác HCD (cgc)
=> MC=CD
Theo câu b, AC là phân giác MCD
=> MCA=DCA
Xét tam giác MAC và tam giác DAC có
MC=CD
MCA=DCA
AC chung
=> tam giác MAC = tam giác DAC(cgc)
=> AMC=ADC=90*
=> AD vg CD mà HE//AD => HE vg CD
Em tham khảo tại đây nhé.
Câu hỏi của Cả cuộc đời này tôi sẽ mãi yêu một người - Toán lớp 7 - Học toán với OnlineMath