Bác chủ cắt một tấm hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 10 2018
Đáp án D
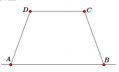
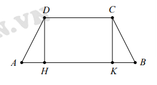Theo bài ra, ta có AD = DC = CB = 4. Đặt AB = x
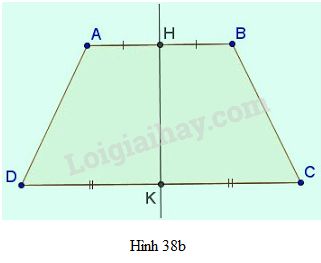
Gọi H, K lần lượt là hình chiếu của D, C trên AB
Vì ABCD là hình thang cân ⇒ AH = BK;CD = HK
Đặt A H = x ⇒ A B = H K + 2 A H = 2 x + 4 và D H = 16 - x 2
Diện tích hình thang cân ABCD là
S A B C D = 1 2 D H . A B + C D = x + 4 16 - x 2 = f x
Xét hàm số f x = x + 4 16 - x 2 trên ( 0 ; 4 ] → m a x ( 0 ; 4 ] f x = 12 3 . Vậy S m a x = 12 3
CM
5 tháng 2 2018
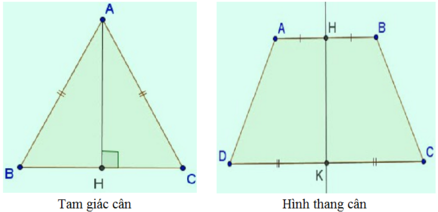
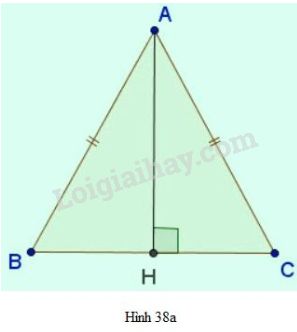
- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).
– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.
CM
21 tháng 9 2019
Đáp án C
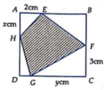
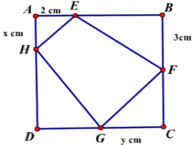
Ta có S E F G H nhỏ nhất ⇔ S = S Δ A E H + S Δ C G F + S Δ D G H lớn nhất (do S Δ B E F không đổi)
⇒ 2 S = 2 x + 3 y + 6 − x 6 − y = x y − 4 x − 3 y + 36 1
Ta có E F G H là hình thang
⇒ A E H ⏜ = C G F ⏜ ⇒ Δ A E H ∽ Δ C G F
⇒ A E C G = A H C F ⇔ 2 y = x 3 ⇒ x y = 6 2
Từ (1), (2) ⇒ 2 S = 42 − 4 x + 18 x
Để 2S lớn nhất thì 4 x + 18 x nhỏ nhất
Mà 4 x + 18 x ≥ 12 2 . Dấu “=” khi
4 x + 18 x ⇔ x = 3 2 2 ⇒ y = 2 2 ⇒ x + y = 7 2 2
CM
20 tháng 3 2017
Ta có SEFGH nhỏ nhất ↔ S = S A E H + S C G F + S D G H lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên A E C G = A H C F ⇒ x y = 6
Từ (1) và (2) suy ra 2S = 42 - ( 4 x - 18 x )
Ta có 2S nhỏ nhất khi và chỉ khi 4 x - 18 x nhỏ nhất.
Biểu thức nhỏ nhất 4 x - 18 x nhỏ nhất ↔ 4 x = 18 x ⇒ x = 3 2 2 ⇒ y = 2 2
Vậy x+y = 3 2 2 + 2 2
Chọn D.
B
21 tháng 4 2017
Chú ý:
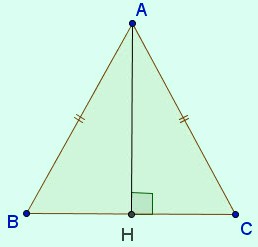
- ∆ABC cân tại A có trục đối xứng là đường phân giác của góc BAC.
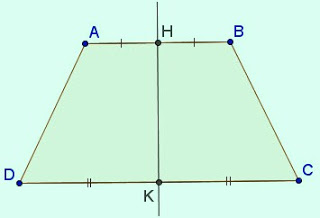
- Hình thang cân nhận đường thẳng đi qua trung điểm hai đáy làm trục đối xứng.
Đối với tam giác cân hình 38a:
# Đối với hình thang cân hình 38b:Tam giác cân ABC, trục đối xứng là đường cao AH với H là trung điểm của đoạn BC.
Hình thang cân ABCD (AB // CD), trục đối xứng là đường thẳng KH với K, H lần lượt là trung điểm của AB và CD.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) AB // A’B’ \( \Rightarrow \) AB // (A’B’C’D’), AD // A’D’ \( \Rightarrow \) AD // (A’B’C’D’)
Do đó (ABCD) // (A’B’C’D’).
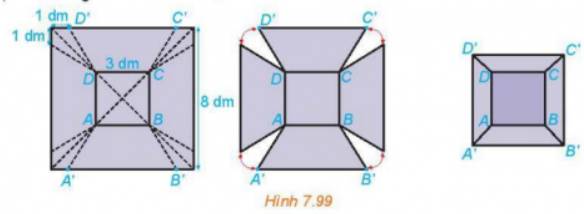
Chiếc thùng có dạng hình chóp cụt vì khi bác Hùng cắt bỏ bốn phần như nhau ở bốn góc của tấm tôn vuông, sẽ tạo thành bốn tam giác vuông cân.
Vậy chiếc thùng có dạng hình chóp cụt.
b) Cạnh bên của hình chóp cụt bằng \(\sqrt {\frac{9}{4} + \frac{{25}}{4}} = \frac{{\sqrt {34} }}{2}\left( {dm} \right)\)
c) Xét mặt chứa đường chéo của hình vuông, nó là hình thang cân có chiều cao bằng chiều cao của hình chóp cụt và được \(h = \sqrt {\frac{{34}}{4} - \frac{{18}}{4}} = 2\left( {dm} \right)\)
Thể tích cần tìm là V = 42 lít.
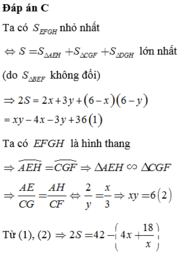
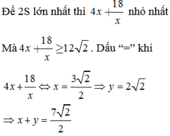
Bạn ghi đề bài cụ thể ra để mọi người giúp đỡ ạ
uh