cho biểu thức A = (x+y) (x-y) + y^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
cho biểu thức A = (x+y) (x-1)+x(2-x-y)+1
a, rút gọn biểu thức
b, tính giá trị biểu thức khi x=1 y=1/2
0
26 tháng 7 2020
a)
*Biểu thức A
Sửa đề: \(A=x\left(x+2\right)+y\left(y-2\right)-2xy+37\)
Ta có: \(A=x\left(x+2\right)+y\left(y-2\right)-2xy+37\)
\(=x^2+2x+y^2-2y-2xy+37\)
\(=x^2+y^2+1+2x-2y-2xy+36\)
\(=\left(x-y+1\right)^2+36\)
Thay x-y=7 vào biểu thức \(A=\left(x-y+1\right)^2+36\), ta được:
\(A=\left(7+1\right)^2+36=8^2+36=100\)
Vậy: 100 là giá trị của biểu thức \(A=x\left(x+2\right)+y\left(y-2\right)-2xy+37\) tại x-y=7
*Biểu thức B
Ta có: \(B=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\)
\(=\left(x^3-3x^2y+3xy^2-y^3\right)-\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3-\left(x-y\right)^2\)
\(=\left(x-y\right)^2\cdot\left(x-y-1\right)\)
Thay x-y=7 vào biểu thức \(B=\left(x-y\right)^2\cdot\left(x-y-1\right)\), ta được:
\(B=7^2\cdot\left(7-1\right)^2=49-36=13\)
Vậy: giá trị của biểu thức \(B=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\) tại x-y=7 là 13
b) Ta có: \(C=x^2+4y^2-2x+10+4xy-4y\)
\(=\left(x^2+4xy+4y^2\right)-\left(2x+4y\right)+10\)
\(=\left(x+2y\right)^2-2\left(x+2y\right)+10\)
\(=\left(x+2y\right)^2-2\cdot\left(x+2y\right)\cdot1+1+9\)
\(=\left(x+2y-1\right)^2+9\)
Thay x+2y=5 vào biểu thức \(C=\left(x+2y-1\right)^2+9\), ta được:
\(C=\left(5-1\right)^2+9=4^2+9=25\)
Vậy: 25 là giá trị của biểu thức \(C=x^2+4y^2-2x+10+4xy-4y\) tại x+2y=5
19 tháng 7 2021
Ta có: \(A=\left(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right):\left(x-y\right)+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\left(x-2\sqrt{xy}+y\right)}{x-y}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\sqrt{x}-\sqrt{y}+2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
=1
20 tháng 11 2023
1: \(C=\left(x-\dfrac{4xy}{x+y}+y\right):\left(\dfrac{x}{x+y}+\dfrac{y}{y-x}+\dfrac{2xy}{x^2-y^2}\right)\)
\(=\dfrac{\left(x+y\right)^2-4xy}{x+y}:\left(\dfrac{x}{x+y}-\dfrac{y}{x-y}+\dfrac{2xy}{\left(x-y\right)\left(x+y\right)}\right)\)
\(=\dfrac{x^2+2xy+y^2-4xy}{x+y}:\dfrac{x\left(x-y\right)-y\left(x+y\right)+2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x^2-2xy+y^2}{x+y}:\dfrac{x^2-xy-xy-y^2+2xy}{\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{\left(x-y\right)^2}{x+y}\cdot\dfrac{x^2-y^2}{x^2-y^2}=\dfrac{\left(x-y\right)^2}{x+y}\)
2: \(\left(x^2-y^2\right)\cdot C=-8\)
=>\(\left(x-y\right)\left(x+y\right)\cdot\dfrac{\left(x-y\right)^2}{x+y}=-8\)
=>\(\left(x-y\right)^3=-8\)
=>x-y=-2
=>x=y-2
\(M=x^2\left(x+1\right)-y^2\left(y-1\right)-3xy\left(x-y+1\right)+xy\)
\(=\left(y-2\right)^2\left(y-2+1\right)-y^2\left(y-1\right)-3xy\left(-2+1\right)+xy\)
\(=\left(y-1\right)\left[\left(y-2\right)^2-y^2\right]+3xy+xy\)
\(=\left(y-1\right)\left(-4y+4\right)+4xy\)
\(=-4\left(y-1\right)^2+4y\left(y-2\right)\)
\(=-4y^2+8y-4+4y^2-8y\)
=-4
H9
HT.Phong (9A5)
CTVHS
6 tháng 12 2023
a) \(B=\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\left(x,y\ge0;x\ne y\right)\)
\(B=\left[\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{x-y}\right]:\dfrac{x-2\sqrt{xy}+y+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)
\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)
\(B=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)
\(B=\dfrac{\sqrt{xy}}{x+\sqrt{xy}+y}\)
b) Xét tử:
\(\sqrt{xy}\ge0\forall x,y\) (xác định) (1)
Xét mẫu:
\(x+\sqrt{xy}+y\)
\(=\left(\sqrt{x}\right)^2+2\cdot\dfrac{1}{2}\sqrt{y}\cdot\sqrt{x}+\left(\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)
\(=\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)
Mà: \(\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2\ge0\forall x,y\) (xác định), còn: \(\dfrac{3}{4}y\ge0\) vì theo đkxđ thì \(y\ge0\) (2)
Từ (1) và (2) ⇒ B luôn không âm với mọi x,y (\(B\ge0\)) (đpcm)
20 tháng 8 2017
a,A=x(x+2)+y(y-2)-2xy+37
A=x2+2x+y2-2y-2xy+37
A=(x2-2xy+y2)+(2x-2y)+37
A=(x-y)2+2(x-y)+37
A=72+2.7+37=49+14+37=100
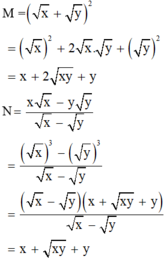
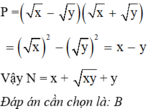
Để đơn giản hóa biểu thức �=(�+�)(�−�)+�2A=(x+y)(x−y)+y2, ta có thể thực hiện các bước như sau:
Bước 1: Áp dụng hằng đẳng thức
Biểu thức (�+�)(�−�)(x+y)(x−y) là một hằng đẳng thức, cụ thể là hằng đẳng thức hiệu bình phương:
(�+�)(�−�)=�2−�2.(x+y)(x−y)=x2−y2.
Bước 2: Thay vào biểu thức
Thay (�+�)(�−�)(x+y)(x−y) bằng �2−�2x2−y2 vào biểu thức ban đầu:
�=(�+�)(�−�)+�2=�2−�2+�2.A=(x+y)(x−y)+y2=x2−y2+y2.
Bước 3: Đơn giản hóa
Lúc này, hai hạng tử −�2−y2 và +�2+y2 sẽ cancel nhau, do đó:
�=�2.A=x2.
Kết quả:
Biểu thức �A sau khi đơn giản hóa là:
�=�2.A=x2.