Để tham gia chương trình tết no ấm học sinh vùng cao , hs lớp 7A, 7B, 7C tổ chức gói bánh trưng. Số bánh trưng lớp 7A và 7B gói được tỉ lệ nghịch với 3 và 2. Số bánh trưng lớp 7B và 7C gói được tỉ lệ nghịch với 7 và 5. Số bánh trưng lớp 7C gói được nhiều hơn lớp 7A là 22 chiếc. Hỏi cả 3 lớp gói được bao nhiêu chiếc bánh trưng để tham gia chương trình này?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
17 tháng 10 2021
Gọi số bánh của 3 lớp 7A,7B,7C lần lượt là x,y,z ta có:
x/11; y/12; z/13
Theo t/c của dãy tỉ số bằng nhau ta có:
x/11=y/12=z/13=(z-x)/(13-11)=12/2=6
=>x=6x11=66
=>y=6x12=72
z=6x13=78
Vậy số bánh trung thu của lớp 7A là:....
7B là:...
7C là;....
14 tháng 6 2022
Gọi số chiếc lớp 7A,7B và 7C gói được lần lượt là a,b,c
Theo đề, ta có:
\(\left\{{}\begin{matrix}3a=2b\\7b=5c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{b}{3}\\\dfrac{b}{5}=\dfrac{c}{7}\end{matrix}\right.\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{21}=\dfrac{c-a}{21-10}=\dfrac{22}{11}=2\)
Do đó: a=20; b=30; c=42
19 tháng 12 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{c-b}{21-10}=2\)
Do đó: a=30; b=20; c=42
24 tháng 4 2023
`@` `\text {dnammv}`
Gọi số vở `3` lớp quyên góp được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Số vở của `3` lớp lần lượt tỉ lệ với số học sinh
Nghĩa là: `x/32=y/35=z/36`
Tổng số vở lớp `7A, 7B` nhiều hơn lớp `7C` là `62` quyển
`-> x+y-z=62`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/32=y/35=z/36=(x+y-z)/(32+35-36)=62/31=2`
`-> x/32=y/35=z/36=2`
`-> x=32*2=64 , y=35*2=70 , z=36*2=72`
Vậy, số vở mà `3` lớp quyên góp được lần lượt là `64, 70, 72 (\text {quyển})`
24 tháng 4 2023
Gọi số quyển vở lớp 7A,7B,7C góp được lần lượt là a,b,c
Theo đề, ta có: a/32=b/35=c/36 và a+b-c=62
=>a/32=b/35=c/36=(a+b-c)/(32+35-36)=62/31=2
=>a=64; b=70; c=72
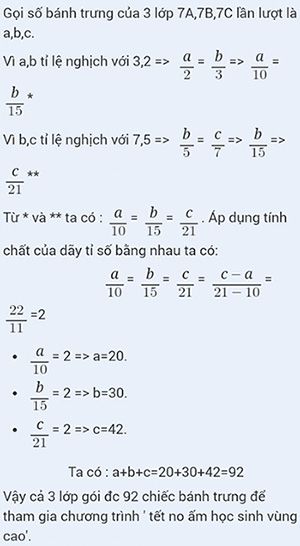
Gọi số bánh trưng của 3 lớp 7A,7B,7C lần lượt là a,b,c.
Vì a,b tỉ lệ nghịch với 3,2 => \(\frac{a}{2}\)= \(\frac{b}{3}\)=> \(\frac{a}{10}\)= \(\frac{b}{15}\)*
Vì b,c tỉ lệ nghịch với 7,5 => \(\frac{b}{5}\)= \(\frac{c}{7}\)=> \(\frac{b}{15}\)=> \(\frac{c}{21}\)**
Từ * và ** ta có : \(\frac{a}{10}\)= \(\frac{b}{15}\)= \(\frac{c}{21}\). Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{10}\)= \(\frac{b}{15}\)= \(\frac{c}{21}\)= \(\frac{c-a}{21-10}\)= \(\frac{22}{11}\)=2
Ta có : a+b+c=20+30+42=92
Vậy cả 3 lớp gói đc 92 chiếc bánh trưng để tham gia chương trình ' tết no ấm học sinh vùng cao'.