Cho tam giác ABC có AB=AC tia phân giác góc A cắt BC tại D. Chứng minh gác ADB < 90 độ < ADC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AB<AC nên góc B>góc C
góc ADB=góc DAC+góc C
góc ADC=góc DAB+góc B
mà góc DAC=góc DAB, góc C<góc B
nên góc ADB<góc ADC

a) Trong \(\Delta ABC\),do AB < AC(gt) nên \(\widehat{C}< \widehat{B}\)(góc đối diện với cạnh lớn hơn là góc lớn hơn)
\(\widehat{ADB},\widehat{ADC}\)theo thứ tự là góc ngoài tại đỉnh D của \(\Delta ADC,\Delta ADB\) ta có :
\(\hept{\begin{cases}\widehat{ADB}=\widehat{C}+\widehat{A_1}\left(1\right)\\\widehat{ADC}=\widehat{B}+\widehat{A_2}\left(2\right)\end{cases}}\)
Vì \(\widehat{C}< \widehat{B}\),còn \(\widehat{A_1}=\widehat{A_2}\)(gt) , do đó từ 1 và 2 => \(\widehat{ADB}< \widehat{ADC}\)
b) Do AB < AC(gt),trên cạnh AC lấy điểm E sao cho AE = AB
Xét \(\Delta ADB\) và \(\Delta ADE\)có :
AD chung
\(\widehat{DAB}=\widehat{DAE}\)
AB = AE(gt)
=> \(\Delta ADB=\Delta ADE\left(c.g.c\right)\)
Nên \(\widehat{AED}=\widehat{B}\) mà \(\widehat{AEB}+\widehat{DEC}=180^0\)(2 góc kề bù),do đó \(\widehat{B}+\widehat{DEC}=180^0\left(3\right)\)
Mặt khác \(\Delta ABC\)thì \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\), do đó \(\widehat{B}+\widehat{C}< 180^0\left(4\right)\)
Từ 3 -> 4 ta có \(\widehat{DEC}>\widehat{C}\)
Trong \(\Delta DEC\)ta có DE < DC,nhưng DE = DB(cạnh tương ứng của hai tam giác bằng nhau : \(\Delta ADB=\Delta ADE\))
Vậy DB < DC hay DC > DB

a, Xét △ABD và △ACD có:
AB=AC(gt)AB=AC(gt)
Aˆ1=Aˆ2A^1=A^2 (vì AD là phân giác của ∠A)
AD chung
⇒ΔABD=ΔACD(c.g.c)⇒ΔABD=ΔACD(c.g.c)
Vậy ΔABD=ΔACD(đpcm)ΔABD=ΔACD(đpcm)
b, Vì △ABD=△ACD (chứng minh trên) nên ta có:
Bˆ=CˆB^=C^ (hai góc tương ứng)
Vậy Bˆ=Cˆ(đpcm)B^=C^(đpcm)
c, Vì △ABD=△ACD (chứng minh trên) nên ta có:
Dˆ1=Dˆ2D^1=D^2 (hai góc tương ứng)
Mà Dˆ1+Dˆ2=1800D^1+D^2=1800 (kề bù)
⇒Dˆ1=Dˆ2=18002=900⇒D^1=D^2=18002=900
Vậy AD⊥BC(đpcm)
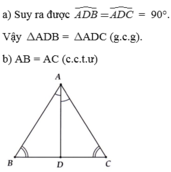
Trong tam giác ABC có AB = AC, tia phân giác góc A cắt BC tại D. Để chứng minh rằng góc ADB < 90 độ và góc ADC > 90 độ, ta làm như sau:
Chứng minh tam giác ADB = tam giác ADC:
Sử dụng tính chất của hai tam giác:
Kết luận:
Vậy ta có chứng minh.
Hãy kiểm tra lại các thông tin quan trọng liên quan đến hình học trong tam giác.