\(\left(x-\dfrac{1}{5}\right)^2+\left(y+0,4\right)^{100}+\left(z-3\right)^{678}=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HN
21 tháng 3 2022
a) m2+1\(\ge\)1 \(\forall\)m, suy ra phương trình đã cho là phương trình bậc nhất một ẩn với mọi m.
b) Nghiệm của phương trình đã cho là x=\(\dfrac{2m}{m^2+1}\) (*).
Áp dụng BĐT Co-si cho hai số dương m2 và 1, ta có:
m2+1\(\ge\)2\(\sqrt{m^2.1}\)=2|m|.
Dấu "=" xảy ra khi và chỉ khi m2=1 \(\Rightarrow\) m=\(\pm\)1.
Với m=1, x=1.
Với m=-1, x=-1.
So sánh hai giá trị của x, ta kết luận: giá trị m cần tìm là m=1.
KT
0

HD
0


21 tháng 1 2016
chuyển hết về qua 1 bên còn về bên kia = 0 sau đó rút gọn rồi đặt nhân tử chung ra và giải như phương trình tích là đc
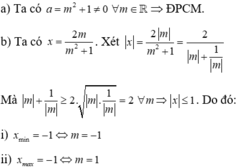


\(\left(x-\dfrac{1}{5}\right)\)2 + (y + 0,4)100 + (z - 3)678 = 0
Vì \(\left(x-\dfrac{1}{5}\right)^2\) ≥ 0; (y + 0,4)100 ≥ 0; (z - 3)678 ≥ 0 ∀ \(x;y;z\)
Vậy \(\left(x-\dfrac{1}{5}\right)^2\) + (y + 0,4)100 + (z - 3)678 = 0 khi và chỉ khi
\(\left\{{}\begin{matrix}x-\dfrac{1}{5}=0\\y+0,4=0\\z-3=0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-0,4\\z=3\end{matrix}\right.\)
Vậy (\(x;y;z\)) = (\(\dfrac{1}{5}\); -0,4; 3)