Cho điểm M nằm trên tia phân giác At của góc xAy nhọn. Kẻ MH vuông góc Ax tại M và MK vuông góc Ay ở K
1) So sánh MH và MK
2) Chứng minh tam giác AMH bằng tam, giác AKM
( Tính chất tia phân giác của góc)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 1 2017
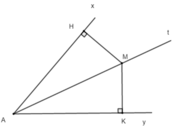
M H ⊥ A x ở H nên MH là khoảng cách từ M đến Ax
M K ⊥ A y ở K nên MK là khoảng cách từ M đến Ay
Mà M thuộc tia phân giác At của góc xAy nên M cách đều hai tia Ax và Ay
Vậy MH = MK.
Chọn đáp án A
DT
20 tháng 3 2019
a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM