vẽ hình và giải chi tiết hộ mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
4H
1
Những câu hỏi liên quan
30 tháng 11 2021
\(b,\text{PT }\left(d_1\right)\text{ giao Oy: }x=0\Leftrightarrow y=2\Leftrightarrow A\left(0;2\right)\\ \text{PT }\left(d_2\right)\text{ giao Oy: }x=0\Leftrightarrow y=-2\Leftrightarrow B\left(0;-2\right)\\ \text{PT hoành độ giao điểm }\left(d_1\right);\left(d_2\right):2x+2=-\dfrac{1}{2}x-2\\ \Leftrightarrow\dfrac{5}{2}x=-4\Leftrightarrow x=-\dfrac{8}{5}\Leftrightarrow y=-\dfrac{6}{5}\Leftrightarrow C\left(-\dfrac{8}{5};-\dfrac{6}{5}\right)\\ c,\text{Vì }2>0\text{ nên góc tạo đc là góc nhọn}\\ \text{Gọi góc đó là }\alpha\left(\alpha< 90\right)\\ \text{Ta có hs góc của }\left(d_1\right)\text{ là }2\\ \Leftrightarrow\tan\alpha=2\approx\tan63^026'\\ \Leftrightarrow\alpha\approx63^026'\)
ND
0
BB
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
1
22 tháng 10 2023
a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)
BB
Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
1
15 tháng 10 2023
a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CDvà BD//CH
BH//CD
AC vuông góc BH
Do đó: CA vuông góc CD
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc AB
=>ΔABD vuông tại B
c: \(\widehat{ABD}=\widehat{ACD}=90^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=ID=IC
25 tháng 12 2022
chỉ tính câu b thôi, hay là bạn cần làm cả bài bạn nhỉ?
HT
0
5 tháng 11 2021
Ta có \(\widehat{S}+\widehat{SGQ}+\widehat{Q}=180^0\Rightarrow\widehat{S}+\widehat{Q}=180^0-\widehat{SGQ}\)
Mà \(\widehat{S}-\widehat{Q}=12^0\Rightarrow\left\{{}\begin{matrix}\widehat{S}=\dfrac{180^0-\widehat{SGQ}+12^0}{2}=96^0-\dfrac{\widehat{SGQ}}{2}\\\widehat{Q}=\dfrac{180^0-\widehat{SGQ}-12^0}{2}=84^0-\dfrac{\widehat{SGQ}}{2}\end{matrix}\right.\)
Mà GP là p/g nên \(\widehat{QGP}=\widehat{PGS}=\dfrac{\widehat{SGQ}}{2}\)
\(\Rightarrow\widehat{Q}=84^0-\widehat{QGP}\)
Ta có \(\widehat{GPS}=\widehat{Q}+\widehat{QGP}=84^0-\widehat{QGP}+\widehat{QGP}=84^0\) (tc góc ngoài)
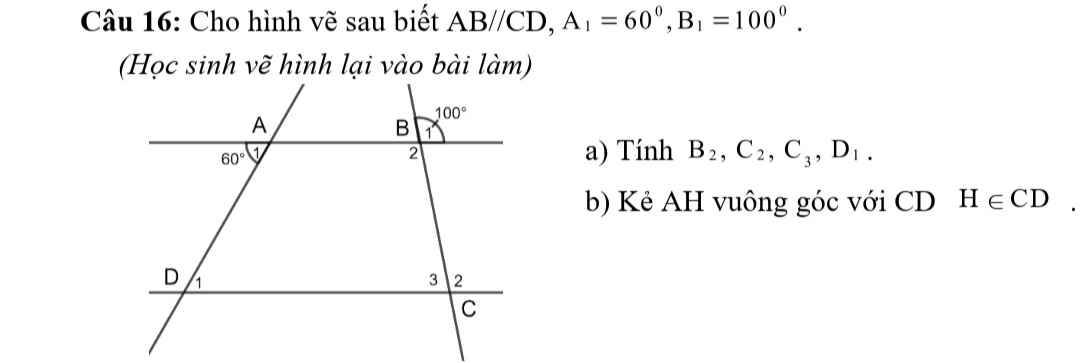
A B C D E F P G O H I
a/
\(\widehat{AOC}=\widehat{COB}=\widehat{BOD}=\widehat{DOA}=90^o\)
\(sđ\widehat{AOC}=sđcungAC\) (góc ở tâm)
\(sđ\widehat{COB}=sđcungCB\) (nt)
\(sđ\widehat{BOD}=sđcungBD\) (nt)
\(sđ\widehat{DOA}=sđcungDA\) (nt)
\(\Rightarrow sđcungDA=sđcungBD\)
Xét \(\Delta DFE\) và \(\Delta DCP\)
\(sđ\widehat{AFD}=\dfrac{1}{2}sđcungDA\) (góc nt)
\(sđ\widehat{BCD}=\dfrac{1}{2}sđcungBD\) (góc nt)
Mà \(sđcungDA=sđcungBD\left(cmt\right)\)
\(\Rightarrow\widehat{AFD}=\widehat{BCD}\)
\(\widehat{CDF}\) chung
\(\Rightarrow\Delta DFE\sim\Delta DCP\left(g.g.g\right)\)
b/
Xét \(\Delta HBD\)
\(AB\perp CD\left(gt\right)\Rightarrow BO\perp DH\)
\(\widehat{CBD}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow BC\perp BD\)
HG//BC (gt)
\(\Rightarrow HG\perp BD\)
=> G là trực tâm của \(\Delta HBD\)
c/