 helpppppppppppppp meeeeeeeeeeeeeeeeeeee
helpppppppppppppp meeeeeeeeeeeeeeeeeeee
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lớp 4A trồng được 96*7/8=84 cây
Lớp 4B trồng được 96-84=12 cây


\(a,\)
\(=4x^2+4x-2xy-2y+x^2+2x+1+4x^2-4xy-y^2\)
\(=9x^2+6x-6xy-2y-y^2+1\)
\(b,\)
\(\dfrac{2x^2+3x-2}{2x-1}=\dfrac{\left(2x^2-x\right)+\left(4x-2\right)}{2x-1}\)
\(=\dfrac{x\left(2x-1\right)+2\left(2x-1\right)}{2x-1}\)
\(=\dfrac{\left(2x-1\right)\left(x+2\right)}{2x-1}\)\(=x+2\)


Thay x = 2 ; y = -1 ta được
\(A=4-3\left(-1\right)+4.4=4+3+16=23\)

ĐKXĐ:\(x\ne-1,x\ne-2\)
\(\dfrac{\left(x+2\right)\left(2x-1\right)-x-2}{x^2+3x+2}=0\\ \Rightarrow2x^2+4x-x-2-x-2=0\\ \Leftrightarrow2x^2+2x-4=0\\ \Leftrightarrow x^2+x-2=0\\ \Leftrightarrow\left(x+2\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy \(x\in\left\{1\right\}\)
Chọn D

Lời giải:
\(B=\frac{2x+\sqrt{x}-4}{(\sqrt{x}+1)(\sqrt{x}-2)}-\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{(\sqrt{x}+1)(\sqrt{x}-2)}+\frac{\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}\)
\(=\frac{2x+\sqrt{x}-4-(x-4)+\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{x+2\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{(\sqrt{x}+1)^2}{(\sqrt{x}+1)(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(P=AB=\frac{3\sqrt{x}-4}{\sqrt{x}+1}.\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{3\sqrt{x}-4}{\sqrt{x}-2}\)
\(P\geq 2\Leftrightarrow \frac{3\sqrt{x}-4}{\sqrt{x}-2}\geq 2\)
\(\Leftrightarrow \frac{3\sqrt{x}-4}{\sqrt{x}-2}-2\geq 0\Leftrightarrow \frac{\sqrt{x}}{\sqrt{x}-2}\geq 0\)
\(\Leftrightarrow \sqrt{x}-2>0\Leftrightarrow x>4\)
Kết hợp với ĐKXĐ suy ra $x>4$


 helpppppppppppppp
helpppppppppppppp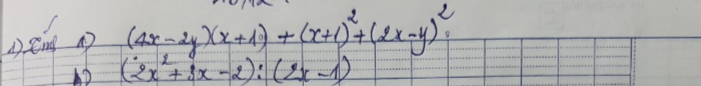


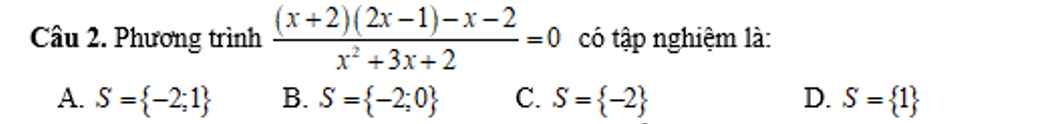

 ý c helpppppppppppppp
ý c helpppppppppppppp
A B C D H
a/
\(B+C=180^o-A=180^o-40^o=140^o\) (Tổng các góc trong của một tg \(=180^o\))
\(B=C\) (góc ở đáy tg cân)
\(\Rightarrow B=C=\dfrac{140^o}{2}=70^o\)
b/ Xét tg vuông ABH và tg vuông ACH có
\(AB=AC\) (cạnh bên tg cân)
\(B=C\left(cmt\right)\)
=> tg ABH = tg ACH (2 tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
c/
Xét tg vuông ABH và tg vuông DCH có
\(HA=HD\left(gt\right)\)
\(\Delta ABH=\Delta ACH\left(cmt\right)\Rightarrow BH=CH\)
\(\Rightarrow\Delta ABH=\Delta DCH\) (2 tg vuông có 2 cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{BAH}=\widehat{CDH}\) mà 2 góc này ở vị trí so le trong
=> AB//CD