2x2 = 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2021
1: \(-x^2+2x+8\)
\(=-\left(x^2-2x-8\right)\)
\(=-\left(x-4\right)\left(x+2\right)\)
2: \(2x^2-3x+1=\left(x-1\right)\left(2x-1\right)\)
4 tháng 3 2022
a, \(P\left(x\right)=5x^5-4x^2+7x+1;Q\left(x\right)=5x^5-4x^2+3x+8\)
b, \(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c, \(P\left(x\right)=Q\left(x\right)\Rightarrow7x+1=3x+8\Leftrightarrow4x=7\Leftrightarrow x=\dfrac{7}{4}\)
4 tháng 3 2022
a/ \(P\left(x\right)=8x^5+7x-6x^2-3x^5+2x^2+1\)
\(=8x^5-3x^5-6x^2+2x^2+7x+1\)
\(=5x^5-4x^2+7x+1\)
\(Q\left(x\right)=4x^5+3x-2x^2+x^5-2x^2+8\)
\(=4x^5+x^5-2x^2-2x^2+3x+8\)
\(=5x^5-4x^2+3x+8\)
b/ \(P\left(x\right)=5x^5-4x^2+7x+1\)
+ \(Q\left(x\right)=5x^5-4x^2+3x+8\)
____________________________
\(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c/ \(P\left(x\right)=Q\left(x\right)\)
\(\Rightarrow5x^5-4x^2+7x+1=5x^5-4x^2+3x+8\)
\(\Rightarrow7x+1=3x+8\)
\(\Rightarrow4x-7=0\)
\(\Rightarrow x=\dfrac{7}{4}\)
TT
2
12 tháng 10 2023
\(\left(x^2+4x+8\right)\left(x^2+5x+8\right)=2x^2\left(1\right)\)
\(\Leftrightarrow x^4+5x^3+8x^2+4x^3+20x^2+32x+8x^2+40x+64-2x^2=0\)
\(\Leftrightarrow x^4+5x^3+4x^3+8x^2+20x^2+8x^2-2x^2+40x+32x+64=0\)
\(\Leftrightarrow x^4+9x^3+34x^2+72x+64=0\)
\(\Leftrightarrow x^4+2x^3+7x^3+14x^2+20x^2+40x+32x+64=0\)
\(\Leftrightarrow x^3\left(x+2\right)+7x^2\left(x+2\right)+20x\left(x+2\right)+32\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3+7x^2+20x+32\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3+4x^2+3x^2+12x+8x+32\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x^2\left(x+4\right)+3x\left(x+4\right)+8\left(x+4\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+4\right)\left(x^2+3x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+4=0\\x^2+3x+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\\vô.nghiệm\left(\Delta=9-32=-23< 0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\) là nghiệm của phương trình \(\left(1\right)\)
22 tháng 8 2021
\(2x^2-6x+8=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}+8=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{2}\)
Vì \(2\left(x-\dfrac{3}{2}\right)^2\ge0\Rightarrow2\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)
\(ĐTXR\Leftrightarrow x=\dfrac{3}{2}\)
Vậy GTNN của \(2x^2-6x+8\) là \(\dfrac{7}{2}\) khi và chỉ khi \(x=\dfrac{3}{2}\)
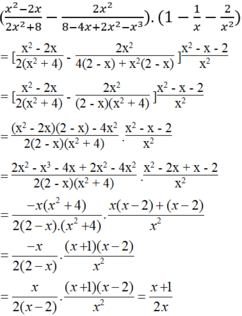
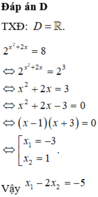
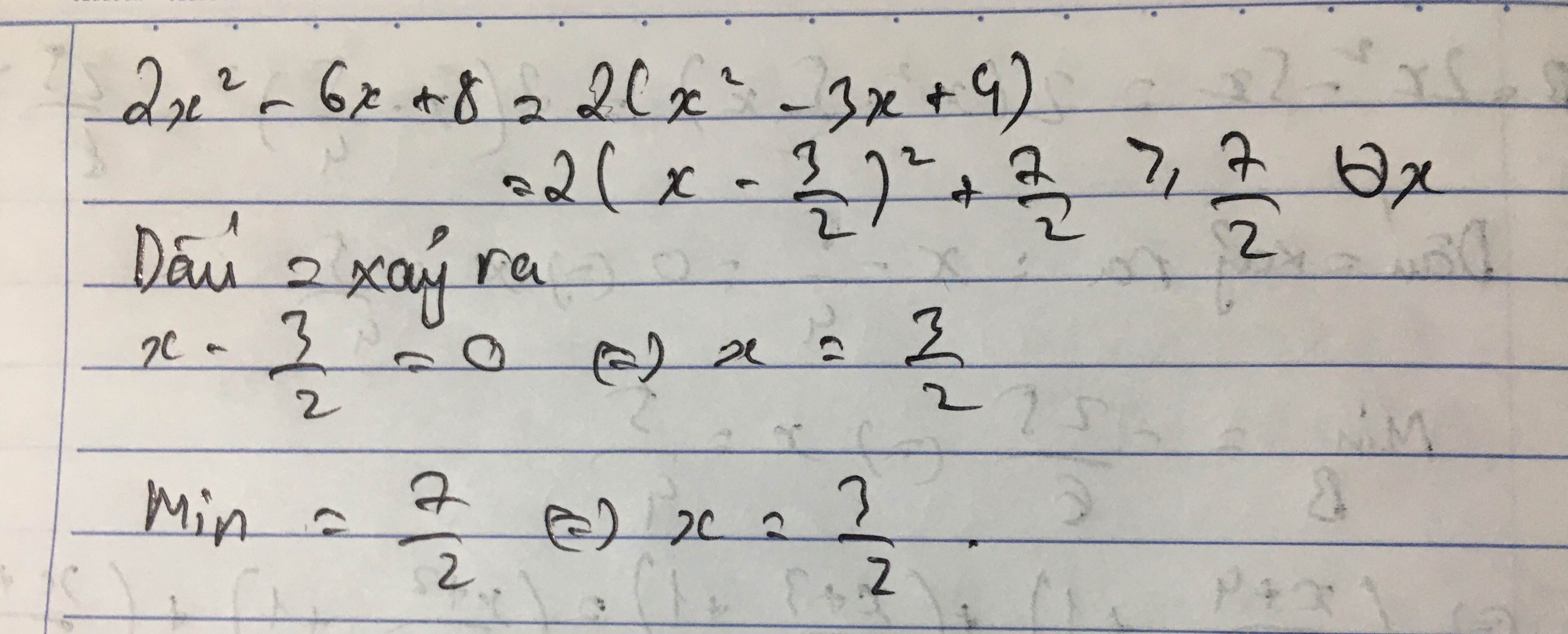
`2x^2 = 8`
`x^2 = 8 : 2`
`x^2 = 4`
`x^2 = (+-2)^2`
`x = +-2`
2x2 = 8
⇒ x2 = 8 : 2
⇒ x2 = 4
Hay x2 = 22
⇒ x = \(\pm\) 2
Vậy x = \(\pm\) 2
Lưu ý : \(\pm\) 2 là 2 và -2