Cô hoài ơi giúp e mấy bài e ms ra ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
13 tháng 7 2023
Hiệu của mẫu số và tử số là 26
Tổng của tử số và mẫu số là:
120 × 2 = 240
Tử số là:
(240 - 26) : 2 = 107
Mẫu số là:
107 + 26 = 133
Phân số cần tìm là 107/133
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
Cô làm rồi em nhá làm theo đúng cách của tiểu học luôn em nha, cảm ơn em đã tin tưởng và yêu thương olm, chúc em học tốt.
https://olm.vn/cau-hoi/cho-phan-so-ab-rut-gon-ab-ta-duoc-phan-so-la-37-neu-dem-tu-so-cua-phan-so-da-cho-cong-voi-25-va-giu-nguyen-mau-so-thi-duoc-phan-so-moi-sau-khi-r.8121397970933
VN
8
HH
1
HH
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 9 2023
A = 1 + 2 + 3 +...+ 50
Dãy số trên là dãy số cách đều với khoảng cách là:
2 - 1 = 1
Số số hạng của dãy số trên là:
(50 - 1): 1 + 1 = 50
Tổng A là:
A = (50 + 1)x 50 : 2 = 1275
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 9 2023
Muốn tính tổng của một dãy số cách đều em cần có kiến thức sau:
1, Tìm khoảng cách của dãy số cách đều bằng cách lấy số hạng sau trừ số hạng liền kề trước nó
2, Tìm số số hạng bằng cách lấy số cuối trừ số đầu được bao nhiêu chia cho khoảng cách rồi cộng 1
3, Tổng dãy số cách đều bằng (số cuối + số đầu) nhân số số hạng rồi chia 2
3N
3
HP
29 tháng 10 2021
1.
- FeCl3
+ Được cấu tạo từ 2 nguyên tố là fe và Cl
+ Có 1 nguyên tử Fe và 3 nguyên tử Cl
+ \(PTK_{FeCl_3}=56+35,5.3=162,5\left(đvC\right)\)
- Zn(HCO3)2
+ Được cấu tạo tử 4 nguyên tố là Zn, H, C và O
+ Có 1 nguyên tử Zn, 2 nguyên tử H, 2 nguyên tử C và 6 nguyên tử O
+ \(PTK_{Zn\left(HCO_3\right)_2}=65+\left(1+12+16.3\right).2=187\left(đvC\right)\)
- C6H12O6
+ Có 3 nguyên tố tạo thành là C, H và O
+ Có 6 nguyên tử C, 12 ngyên tử H và 6 nguyên tử O
+ \(PTK_{C_6H_{12}O_6}=12.6+1.12+16.6=180\left(đvC\right)\)
2.
Lần lượt: Fe(III), C(IV)
3.
a. CaO
b. Mg3(PO4)2
c. H2SO4
29 tháng 10 2021
2. \(Fe_2O_3\) CÓ HÓA TRỊ lll.
\(CH_4\) có hóa trị lV.
3.a)\(CaO\)
b)\(Mg_3\left(PO_4\right)_2\)
c)\(H_2SO_4\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 7 2023
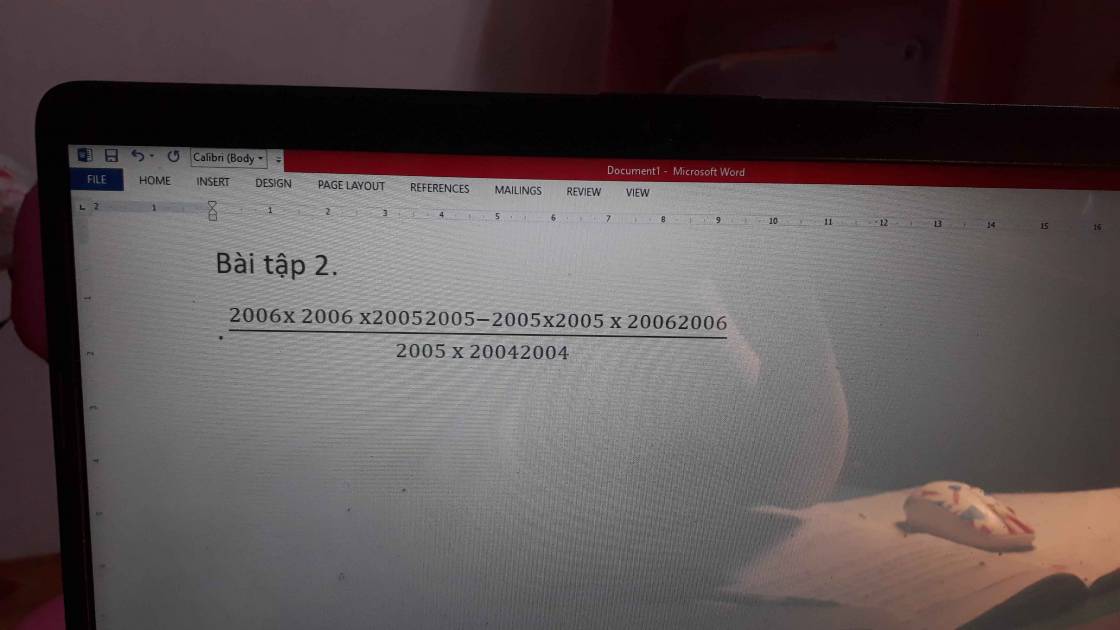
\(\dfrac{2006\times2006\times20052005-2005\times2005\times20062006}{2005\times20042004}\)
= \(\dfrac{2006\times2006\times2005\times10001-2005\times2005\times2006\times10001}{2005\times2004\times10001}\)
= \(\dfrac{2005\times2006\times10001\times\left(2006-2005\right)}{2005\times2004\times10001}\)
= \(\dfrac{2005\times10001\times2\times1003}{2005\times10001\times2\times1002}\)
= \(\dfrac{1003}{1002}\)
25 tháng 7 2023
$dfrac{2006\times2006\times20052005-2005\times2005\times20062006}{2005\times2024024}$
$=\dfrac{2006\times2006\times2005\times10001-2005\times2005\times2006\times10001}{2005\times2004\times10001}$
$=\dfrac{(2006\times2006\times2005-2005\times2005\times2006)\times10001}{2005\times2004\times10001}$
$=\dfrac{[2005\times(2006\times2006-2005\times2006)]\times10001}{2005\times2004\times10001}$
$=\dfrac{2005\times[2006\times(2006-2005)]\times10001}{2005\times2004\times10001}$
$=\dfrac{2005\times(2006\times1)\times10001}{2005\times2004\times10001}$
$=\dfrac{2005\times2006\times10001}{2005\times2004\times10001}$
$=\dfrac{2006}{2004}=\dfrac{1003{1002}$
LN
2
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2024
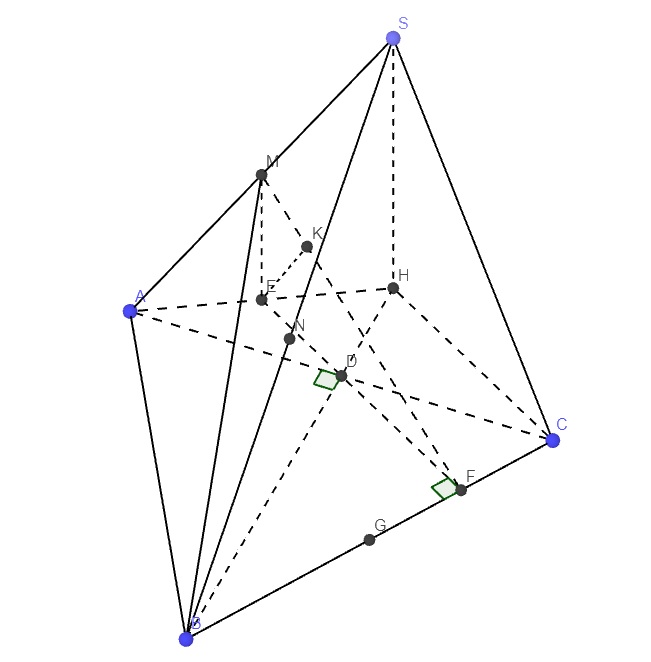
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)
Tên cô bạn phải viết hoa , nhớ là phải tôn trọng cô nhé !