cho tam giác abc có ab = ac tia phân giác góc a cắt bc tại d .chứng minh rằng góc b = c và bd= cd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 1 2017
1. A B C D F 1 2 2 1 1 2. A B H D M C
1.Lấy F trên AC sao cho AB = AF mà AB < AC => AF < AC => F nằm giữa A,C
\(\Delta ADB,\Delta ADF\)có AD chung ; AB = AF ;\(\widehat{A_1}=\widehat{A_2}\)(AD là phân giác góc BAC)\(\Rightarrow\Delta ADB=\Delta ADF\left(c.g.c\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{D_2}\); DB = DF mà\(\widehat{F_1}>\widehat{D_1};\widehat{D_2}>\widehat{C}\)(\(\widehat{F_1};\widehat{D_1}\)lần lượt là góc ngoài\(\Delta ADF,\Delta ADC\))nên\(\widehat{F_1}>\widehat{C}\)
\(\Delta DFC\)có\(\widehat{F_1}>\widehat{C}\)nên DC > DF = DB.Vậy BD < CD
2.Theo chứng minh câu 1,ta được BD < CD
\(\Rightarrow BC=BD+CD=2BD+CD-BD\Rightarrow2BD< BC\Rightarrow BD< \frac{BC}{2}\left(=BM\right)\)
=> D nằm giữa B,M => AD nằm giữa AB,AM (1)
\(\Delta ABC\)có AB < AC nên\(\widehat{B}>\widehat{C}\)mà\(\widehat{BAH}=90^0-\widehat{B};\widehat{CAH}=90^0-\widehat{C}\)(vì\(\Delta AHB,\Delta AHC\)vuông tại H)
\(\Rightarrow\widehat{BAH}< \widehat{CAH}\)
\(\Rightarrow\widehat{BAC}=\widehat{BAH}+\widehat{CAH}=2\widehat{BAH}+\widehat{CAH}-\widehat{BAH}\Rightarrow2\widehat{BAH}< \widehat{BAC}\Rightarrow\widehat{BAH}< \frac{\widehat{BAC}}{2}\left(=\widehat{BAD}\right)\)
=> AH nằm giữa AB,AD (2).Từ (1) và (2),ta có đpcm
8 tháng 12 2016
cái này dẽ mà chỉ càn chứng minh 2 tam giác có chứa 2 cạnh đó bằng nhau là được
TN
8 tháng 12 2016
Xét tam giác ABD và tam giác ACD ta có:
Góc BAD = góc CAD (t/chất tia phân giác)
AD cạnh chung
Góc B = góc C (gt)
=> Tam giác ABD = tam giác ACD (g.c.g)
=> BD = DC (2 cạnh tương ứng)
AB = AC (2 cạnh tương ứng)
Mấy bài này cũng dễ mà, tự động não k đc à?
26 tháng 1 2022
a: Xét ΔABC có BD là đường phân giác
nên AB/BC=AD/DC
=>AD/DC=AC/BC(1)
Xét ΔABC có CE là đường phân giác
nên AE/EB=AC/BC(2)
Từ (1) và (2) suy ra AD/DC=AE/EB
=>ED//BC
=>\(\widehat{EDB}=\widehat{DBC}\)
mà \(\widehat{DBC}=\widehat{EBD}\)
nên \(\widehat{EDB}=\widehat{EBD}\)
b: Xét ΔABC có DE//BC
nên AE/AB=AD/AC
mà AB=AC
nên AE=AD
hay ΔADE cân tại A
30 tháng 4 2022
a: XétΔABC có AD là phân giác
nên DB/CD=AB/AC=3/4(1)
b: Xét ΔCAB có ED//AB
nên ED/EC=AB/AC(2)
từ (1) và (2) suy ra BD/CD=ED/EC
hay \(BD\cdot EC=ED\cdot CD\)
PT
1
CM
1 tháng 4 2017
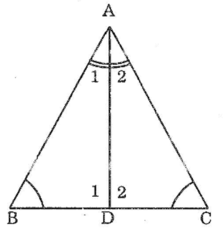
Trong ΔADB, ta có:
∠B +∠(A1 ) +∠(D1) =180o (tổng 3 góc trong tam giác)
Suy ra: ∠(D1 ) =180o-(∠B +(A1)) (1)
Trong ΔADC, ta có:
∠C +∠(A2) +∠(D2) =180o (tổng 3 góc trong tam giác)
Suy ra: ∠(D2) =180o-(∠C +∠(A2) ) (2)
+) Lại có: ∠B =∠C (gỉa thiết)
∠(A1 ) =∠(A2) (vì AD là tia phân giác của góc BAC) (3)
Từ (1), (2) và (3) suy ra: ∠(D1) =∠(D2)
Xét ΔABD và ΔACD, ta có:
∠(A1 ) =∠(A2) ( Vì AD là tia phân giác của góc BAC)
AD cạnh chung
∠(D1 ) =∠(D2) ( chứng minh trên).
Vậy: ΔABD= ΔACD (g.c.g)
Vậy: AB = AC (hai cạnh tương ứng)
DB = DC (hai cạnh tương ứng)
3 tháng 12 2023
a: Kẻ DK\(\perp\)BC
Xét ΔBAD vuông tại A và ΔBKD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)
Do đó: ΔBAD=ΔBKD
=>BA=BK
mà \(BA=\dfrac{1}{2}BC\)
nên \(BK=\dfrac{1}{2}CB\)
=>K là trung điểm của BC
Xét ΔDBC có
DK là đường cao
DK là đường trung tuyến
Do đó: ΔDBC cân tại D
b: ΔDBC cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)
=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)
=>\(\widehat{ABC}=90^0:\dfrac{3}{2}=90^0\cdot\dfrac{2}{3}=60^0\)
\(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}=\dfrac{1}{2}\cdot60^0=30^0\)
27 tháng 1 2022
b: Xét ΔABD và ΔACE có
\(\widehat{BAD}\) chung
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
c: Xét ΔABC có
AE/AB=AD/AC
Do đó: DE//BC
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Xét ΔABC có AB=AC
nên ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
Xét ΔBAD và ΔCAD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔBAD=ΔCAD
=>BD=CD
VậyB=C và BD=CD