d) x-1/8 = 8/x-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= x2+x-2-x+4
=x2+2
Vì x2 >=0 => x2+2>0
Vậy pj]ơng trình vô nghiệm.

đặt x^2+ax+b= (x-1)(x-m)
x^2+ax+b/x^2-1 = x-m/x+1
lim x-m/x+1=-1/2 suy ra 1-m/2=-1/2 nên m = 3
x^2+ax+b= (x-1)(x-3)=x^2-4x+3 suy ra a=-4, b=3

\(\dfrac{6\times8\times11}{66\times4}=\dfrac{6\times4\times2\times11}{6\times11\times4}=2\)

\(-\left(x-1\right)\left(x+4\right)\le0\)
\(\Rightarrow x+4\le0\)
\(\Rightarrow x\le-4\)
a)=0 trước nhé
\(\Rightarrow\orbr{\begin{cases}-\left(x-1\right)=0\\x+4=0\end{cases}}\Rightarrow\orbr{\begin{cases}-x+1=0\\x=-4\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=4\end{cases}}\)
<0 nè
=>-(x-1);x+4 trái dấu;mọi x
ta có
x+4+x-1=2x+3
chịu

\(\Delta'=\left(m-1\right)^2-2\left(m^2-1\right)=-m^2-2m+3>0\)
\(\Rightarrow-3< m< 1\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\left(m-1\right)\\x_1x_2=\dfrac{m^2-1}{2}\end{matrix}\right.\)
\(P=\left(x_1-x_2\right)^2=x_1^2+x_2^2-2x_1x_2\)
\(P=x_1^2+x_2^2+2x_1x_2-4x_1x_2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(P=\left(m-1\right)^2-4\left(\dfrac{m^2-1}{2}\right)\)
\(P=-m^2-2m+3=-\left(m^2+2m+1\right)+4\)
\(P=-\left(m+1\right)^2+4\le4\)
\(P_{max}=4\) khi \(m+1=0\Leftrightarrow m=-1\) (thỏa mãn)

\(\left|2x-1\right|=\dfrac{3}{2}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{3}{2}\\2x-1=-\dfrac{3}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Thay \(x=\dfrac{5}{4}\) vào D ta có:
\(D=4x+3=4.\dfrac{5}{4}+3=5+3=8\)
Thay \(x=-\dfrac{1}{4}\) vào D ta có:
\(D=4.\dfrac{-1}{4}+3=-1+3=2\)
Để \(D=\dfrac{3}{2}\)
\(\Leftrightarrow4x+3=\dfrac{3}{2}\\ \Leftrightarrow4x=-\dfrac{3}{2}\\ \Leftrightarrow x=-\dfrac{3}{8}\)

a: Ta có: \(A=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1\ge1\forall x\)
Dấu '=' xảy ra khi x=10

Lời giải:
PT hoành độ giao điểm: $mx^2=x-2$
$\Leftrightarrow mx^2-x+2=0(*)$
Để 2 đths cắt nhau tại 2 điểm phân biệt thì pt $(*)$ phải có 2 nghiệm phân biệt
Điều này xảy ra khi \(\left\{\begin{matrix} m\neq 0\\ \Delta=1-8m>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ m< \frac{1}{8}\end{matrix}\right.(I)\)
Hoành độ giao điểm khi đó là 2 nghiệm $x_1,x_2$ của pt $(*)$
Áp dụng định lý Viet: $x_1+x_2=\frac{1}{m}; x_1x_2=\frac{2}{m}$
Để 2 điểm phân biệt nằm ở 2 phía của trục tung thì $x_1,x_2$ trái dấu
Tức là $x_1x_2<0\Leftrightarrow\frac{2}{m}<0$
$\Leftrightarrow m<0$
Kết hợp với $(I)$ suy ra $m<0$
\(Bước 1\) Lập phương trình hoành độ
Hoành độ giao điểm là nghiệm của pt
\(x-2=mx^2\\ \Leftrightarrow-mx^2+x-2=0\)
\(Bước2\) Để hai hàm số cắt nhau tại hai điểm phân biệt nằm về hai phía của trục tung => pt có 2 nghiệm trái dấu
\(a\times c< 0\\ \Leftrightarrow\left(-m\right).\left(-2\right)< 0\\ \Leftrightarrow2m< 0\\ \Leftrightarrow m< 0\\ =>B\)

Ta có: \(f\left(x\right)=y=\frac{x^2+mx}{1-x}\Rightarrow y'=\frac{\left(2x+mx\right)\left(1-x\right)+\left(x^2+mx\right)}{\left(1-x\right)^2}=\frac{-x^2+2x+m}{\left(1-x\right)^2}\)\(\)\(\left(D=R/\left\{1\right\}\right)\)
Đặt \(g\left(x\right)=-x^2+2x+m\)\(\Rightarrow\)f(x) cùng dấu với y' trên D
Xét pt g(x)=0
\(\Delta'=m+1\), Hàm số có 2 điểm cực trì<=> pt có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ne0\end{cases}\Leftrightarrow m>-1}\)
Khi đó 2 điểm cực trì là A(x1,f(x1) ) và B(x2, f(x2) )
Lại có \(f'\left(x_1\right)=\frac{\left(2x_1+m\right)\left(1-x_1\right)+\left(x_1^2+mx_1\right)}{\left(1-x_1\right)^2}=0\Rightarrow x_1^2+mx_1=-\left(2x_1+m\right)\left(1-x_1\right)\)
\(\Rightarrow f\left(x_1\right)=\frac{x_1^2+mx_1}{1-x_1}=-2x_1-m.\)
=>\(f\left(x_2\right)=-2x_2-m\)
Khoảng cách giữa 2 điểm cực trị:
\(AB=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{\left(x_1-x_2\right)^2+\left(2x_1-2x_2\right)^2}=|x_1-x_2|\sqrt{5}=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=20\)
A/d Vi-ét cho pt g(x)=0\(\Rightarrow4+4m=20\Leftrightarrow m=4\)
Vậy m=4


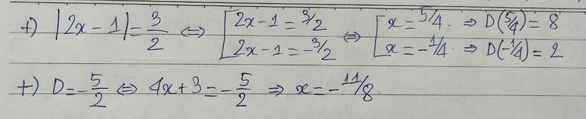
ĐKXĐ: x<>1
\(\dfrac{x-1}{8}=\dfrac{8}{x-1}\)
=>\(\left(x-1\right)\cdot\left(x-1\right)=8\cdot8\)
=>\(\left(x-1\right)^2=64\)
=>\(\left[{}\begin{matrix}x-1=8\\x-1=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8+1=9\left(nhận\right)\\x=-8+1=-7\left(nhận\right)\end{matrix}\right.\)
\(\dfrac{x-1}{8}\) = \(\dfrac{8}{x-1}\) (đk \(x-1\ne0\) ⇒ \(x\ne\) 1)
(\(x-1\)).(\(x-1\)) = 8.8
(\(x-1\))2 = 82
\(\left[{}\begin{matrix}x-1=-8\\x-1=8\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-8+1\\x=8+1\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-7\\x=9\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-7; 9)