Bài 5. (1 điểm)
Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng $72$ m$^3$. Đáy bể có dạng hình chữ nhật với chiều rộng là $x$ (m), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì $x$ phải bằng bao nhiêu (kết quả làm tròn đến hàng phần...
Đọc tiếp
Bài 5. (1 điểm)
Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng $72$ m$^3$. Đáy bể có dạng hình chữ nhật với chiều rộng là $x$ (m), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì $x$ phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
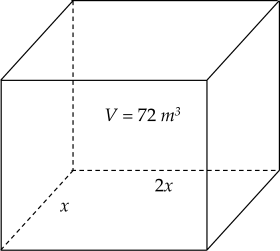

Diện tích đáy bể là: \(2x^2\) `(m^2)`
Chiều cao bể là: \(\dfrac{72}{2x^2}=\dfrac{36}{x^2}\left(m^2\right)\)
Diện tích xung quanh bể là: \(\left(2x+x\right).2.\dfrac{36}{x^2}=\dfrac{216}{x}\left(m^2\right)\)
Diện tích cần xây là:
\(2x^2+\dfrac{216}{x}=2\left(x^2+\dfrac{54}{x}+\dfrac{54}{x}\right)\ge2.3\sqrt[3]{x^2.\dfrac{54}{x}.\dfrac{54}{x}}=54\sqrt[3]{4}\left(m^2\right)\)
Dấu "=" xảy ra khi \(x^2=\dfrac{54}{x}\Rightarrow x=\sqrt[3]{54}=3,78\left(m\right)\)