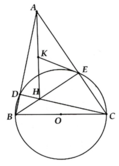
Bài 8. Cho đường tròn (O) bán kính R và một điểm 4 sao cho OA = 2R Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp . Đường thẳng OA cắt BC tại H, cất cung nhỏ và cung lớn BC lần lượt tại 1 và K.
a) Chứng minh OA vuông góc với BC và HI. OA = R ^ 2
b) Chứng minh tam giác ABC đều và ABKC là hình thoi.
c) Chứng minh 1 là tâm đường tròn ngoại tiếp tam giác ABC. Tính theo R bán kính đường tròn...
Đọc tiếp
Bài 8. Cho đường tròn (O) bán kính R và một điểm 4 sao cho OA = 2R Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp . Đường thẳng OA cắt BC tại H, cất cung nhỏ và cung lớn BC lần lượt tại 1 và K.
a) Chứng minh OA vuông góc với BC và HI. OA = R ^ 2
b) Chứng minh tam giác ABC đều và ABKC là hình thoi.
c) Chứng minh 1 là tâm đường tròn ngoại tiếp tam giác ABC. Tính theo R bán kính đường tròn này.
d) Vẽ đường kính CD. Chứng minh BD song song với AO.
e) Vẽ cát tuyến bất kỳ AMN của (O;R). Gọi E là trung điểm của MN. Chứng minh năm điểm O, E, A, B, C cùng thuộc một đường tròn
O A B C H I K D M N E
a/
Xét tg vuông ABO và tg vuông ACO có
OB=OC=R; OA chung => tg ABO = tg ACO (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
Xét tg ABC có
AB=AC (2 tiếp tuyến cùng xp từ 1 điểm...) => tg ABC cân tại A
tg ABO = tg ACO (cmt) \(\Rightarrow\widehat{OAB}=\widehat{OAC}\)
\(\Rightarrow OA\perp BC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Xét tg vuông ABO có
\(OB^2=R^2=OH.OA\) (Hệ thức lượng trong tg vuông)
OA=2R (gt); OI=R => AI=R => AI=OI=R => BI=OA/2=R
c/m tương tự khi xét tg vuông ACO ta cũng có CI=R
Xét tứ giác BOCI có
BI=CI=OB=OC=R => BOCI là hình thoi => OH=HI (trong hình thoi 2 đường chéo cắt nhau tại trung điểm mỗi đường)
\(\Rightarrow OH.OA=HI.OA=OB^2=R^2\)
b/
Xét tg vuông AOB có
\(\sin OAB=\dfrac{OB}{OA}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{OAB}=30^o\)
Ta có \(\widehat{OAC}=\widehat{OAB}\left(cmt\right)\Rightarrow\widehat{OAC}=\widehat{OAB}=30^o\)
\(\Rightarrow\widehat{BAC}=\widehat{OAB}+\widehat{OAC}=30^o+30^o=60^o\)
Xét tg cân ABC có
\(\widehat{ABC}=\widehat{ACB}=\alpha\)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}=180^o-60^o=120^o\)
\(\Rightarrow2\alpha=120^o\Rightarrow\alpha=60^o\)
=> ABC là tg đều
Ta có
OH=HI (cmt)
AI=R(cmt); OK=R
\(\Rightarrow AI+HI=OK+OH\Rightarrow AH=KH\)
Xét tg cân ABC có
\(OA\perp BC\left(cmt\right)\)
=> BH=CH (Trong tg cân đường cao xp từ đỉnh tg cân đồng thời là đường trung tuyến)
=> ABKC là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Mà \(OA\perp BC\Rightarrow AK\perp BC\)
=> ABKC là hình thoi (hbh có 2 đường chéo vuông góc)
c/
Ta có AI=BI=CI=R (cmt) => I là tâm đường tròn ngoại tiếp tg ABC
d/
Xét (O) có
\(\widehat{CBD}=90^o\) (Góc nt chắn nửa đường tròn) \(\Rightarrow BD\perp BC\)
\(OA\perp BC\left(cmt\right)\)
=> BD//AO (cùng vuông góc với BC)
e/
Xét tg OMN có
OM=ON=R
ME=NE (gt)
\(\Rightarrow OE\perp MN\) (Trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
=> B; C; E cùng nhìn AO dưới các góc = nhau và \(=90^o\)
=> B; C; E nằm trên dường tròn đường kính AO => O; E; A; B; C cùng thuộc một đường tròn
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có \(cosBOA=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔOBI có OB=OI và \(\widehat{BOI}=60^0\)
nên ΔOBI đều
ΔOBI đều
mà BH là đường cao
nên H là trung điểm của OI
=>OH=HI
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(HI\cdot OA=R^2\)
b: Xét ΔAOB vuông tại B có \(sinBAO=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
Ta có: HO+OK=HK
HI+IA=HA
mà HO=HI và OK=IA(=R)
nên HK=HA
=>H là trung điểm của KA
Xét tứ giác ABKC có
H là trung điểm chung của AK và BC
=>ABKC là hình bình hành
Hình bình hành ABKC có AB=AC
nên ABKC là hình thoi
c: Ta có: \(\widehat{ABI}+\widehat{OBI}=\widehat{ABO}=90^0\)
\(\widehat{HBI}+\widehat{OIB}=90^0\)(ΔBHI vuông tại H)
mà \(\widehat{OBI}=\widehat{OIB}\left(=60^0\right)\)
nên \(\widehat{ABI}=\widehat{HBI}\)
=>BI là phân giác của góc ABH
d: Xét (O) có
ΔBCD nội tiếp
CD là đường kính
Do đó: ΔBCD vuông tại B
=>BC\(\perp\)BD
mà BC\(\perp\)OA
nên BD//OA
e: ΔOMN cân tại O
mà OE là đường trung tuyến
nên OE\(\perp\)MN tại E
Ta có: \(\widehat{OEA}=\widehat{OBA}=\widehat{OCA}=90^0\)
=>O,E,A,B,C cùng thuộc đường tròn đường kính OA