Tìm x ϵ N, sao cho:
a) x(2x - 10) = 0
b) (x + 1). (x - 2) = 0
c) \(\left(9-x\right)^3\)= 64
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 9 2023
Bài 4:
1,
\(Ư\left(250\right)=\left\{1;2;5;10;25;50;125;250\right\}\)
Các số có hai chữ số thuộc Ư(250) là 10;25;50
2,
\(B\left(11\right)=\left\{0;11;22;33;44;55;66;77;88;99;110;121;132;143;154;165;....\right\}\)
Các số có hai chữ số thuộc về B(11) là 11;22;33;44;55;66;77;88;99
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 9 2023
Bài 3:
B(3) là các số chia hết cho 3, dấu hiệu là tổng các chữ số của số đó là một số chia hết cho 3, bao gồm: 126; 201; 312; 345; 501; 630
B(5) là các số chia hết cho 5, dấu hiệu tận cùng các số đó là 0 hoặc 5, bao gồm: 125; 205; 220; 345; 595; 630; 1780
29 tháng 11 2016
a, Vì : \(6⋮x-1\Rightarrow x-1\inƯ\left(6\right)\)
Mà : \(Ư\left(6\right)=\left\{1;2;3;6\right\}\Rightarrow x\in\left\{2;3;4;7\right\}\)
Vậy ...
b,Vì : \(14⋮2x+3\Rightarrow2x+3\inƯ\left(14\right)\)
Mà : \(Ư\left(14\right)=\left\{1;2;7;14\right\}\) ; \(2x+3\ge3\Rightarrow2x+3\in\left\{7;14\right\}\)
Ta có : 2x + 3 là số lẻ
=> 2x + 3 = 7
=> 2x = 4 => x = 2
Vậy x = 2
c, \(x-1⋮12\Rightarrow x-1\in B\left(12\right)\)
Mà : \(B\left(12\right)=\left\{0;12;24;36;...\right\}\) ; 0 < x < 30
\(\Rightarrow x-1\in\left\{12;24\right\}\)
\(\Rightarrow x\in\left\{13;25\right\}\)
Vậy ...
HQ
Hà Quang Minh
Giáo viên
2 tháng 8 2023
\(a,\left(x-1\right)^2=0\\ \Leftrightarrow x=1\\ b,\left(x-3\right)^2=1\\ \Leftrightarrow\left[{}\begin{matrix}x-3=1\\x-3=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
2 tháng 8 2023
a) \(\left(x-1\right)^2=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
b) \(\left(x-3\right)^2=1\)
\(\Rightarrow\left(x-3\right)^2=1^2\)
\(\Rightarrow\left[{}\begin{matrix}x-3=-1\\x-3=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
12 tháng 9 2016
Bài 1:
a) (2x-3). (x+1) < 0
=>2x-3 và x+1 ngược dấu
Mà 2x-3<x+1 với mọi x
\(\Rightarrow\begin{cases}2x-3< 0\\x+1>0\end{cases}\)
\(\Rightarrow\begin{cases}x< \frac{3}{2}\\x>-1\end{cases}\)\(\Rightarrow-1< x< \frac{3}{2}\)
b)\(\left(x-\frac{1}{2}\right)\left(x+3\right)>0\)
\(\Rightarrow x-\frac{1}{2}\) và x+3 cùng dấu
Xét \(\begin{cases}x-\frac{1}{2}>0\\x+3>0\end{cases}\)\(\Rightarrow\begin{cases}x>\frac{1}{2}\\x>-3\end{cases}\)
Xét \(\begin{cases}x-\frac{1}{2}< 0\\x+3< 0\end{cases}\)\(\Rightarrow\begin{cases}x< \frac{1}{2}\\x< -3\end{cases}\)
=>....
Bài 2:
\(S=\frac{1}{2}\left(\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{999.1001}\right)\)
\(=\frac{1}{2}\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{999}-\frac{1}{1001}\right)\)
\(=\frac{1}{2}\left(\frac{1}{3}-\frac{1}{1001}\right)\)
\(=\frac{1}{2}\cdot\frac{998}{3003}\)
\(=\frac{499}{3003}\)
NQ
11
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: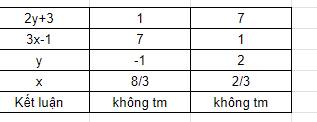
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
H9
HT.Phong (9A5)
CTVHS
28 tháng 10 2023
3/ Ta có:
\(A=\dfrac{1-2x}{x+3}\)
\(A=\dfrac{-2x+1}{x+3}\)
\(A=\dfrac{-2x-6+7}{x+3}\)
\(A=\dfrac{-2\left(x+3\right)+7}{x+3}\)
\(A=-2+\dfrac{7}{x+3}\)
A nguyên khi \(\dfrac{7}{x+3}\) nguyên
⇒ 7 ⋮ \(x+3\)
\(\Rightarrow x+3\inƯ\left(7\right)\)
\(\Rightarrow x+3\in\left\{1;-1;7;-7\right\}\)
\(\Rightarrow x\in\left\{-2;-4;4;-10\right\}\)
TL
0
a; \(x\)(2\(x\) - 10) = 0
\(\left[{}\begin{matrix}x=0\\2x-10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=\dfrac{10}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
Vậy \(x\) \(\in\) {0; 5}
b; (\(x+1\)).(\(x-2\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Vì \(x\) \(\in\) N nên \(x=-1\) loại
Vậy \(x\) = 2