Cho hình vuông ABCD.Trên các cạnh AB,BC,CD,DA lần lượt lấy các điểm M,N,P,Q sao cho AM=BN=CP=DQ
a,C/m △QAM=△NCP
b,C/m MNPQ là hình vuông
Giúp mik nhanh vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 11 2023
1: AM+MB=AB
BN+NC=BC
CP+PD=CD
QD+QA=AD
mà AB=BC=CD=AD và AM=BN=CP=QD
nên BM=CN=PD=QA
2: Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có
MA=NB
AQ=BM
Do đó: ΔMAQ=ΔNBM
=>MQ=MN(1)
Xét ΔMBN vuông tại B và ΔNCP vuông tại C có
MB=NC
BN=CP
Do đó: ΔMBN=ΔNCP
=>MN=NP(2)
Xét ΔNCP vuông tại C và ΔPDQ vuông tại D có
NC=PD
CP=DQ
Do đó: ΔNCP=ΔPDQ
=>NP=PQ(3)
Từ (1),(2),(3) suy ra MQ=MN=NP=PQ
ΔMAQ=ΔNBM
=>\(\widehat{AMQ}=\widehat{BNM}\)
mà \(\widehat{BNM}+\widehat{BMN}=90^0\)(ΔBMN vuông tại B)
nên \(\widehat{AMQ}+\widehat{BMN}=90^0\)
\(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)
=>\(90^0+\widehat{QMN}=180^0\)
=>\(\widehat{QMN}=90^0\)
Xét tứ giác MNPQ có
MN=NP=PQ=MQ
nên MNPQ là hình thoi
Hình thoi MNPQ có \(\widehat{QMN}=90^0\)
nên MNPQ là hình vuông
DY
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 6 2023
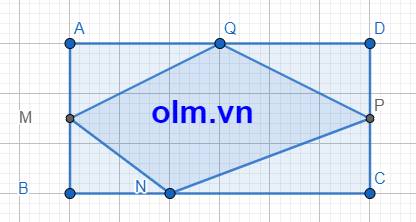
AM = BM = \(\dfrac{1}{2}\)AB; AQ = QD = \(\dfrac{1}{2}\) AD
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ =\(\dfrac{1}{2}\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{8}\)SABCD = 240\(\times\)\(\dfrac{1}{8}\)=30(cm2)
DQ = QA = \(\dfrac{1}{2}\)AD; DP = PC = \(\dfrac{1}{2}\) DC
SDPQ =\(\dfrac{1}{2}\times\)DP\(\times\) DQ =\(\dfrac{1}{2}\) \(\times\)\(\dfrac{1}{2}\)AD\(\times\)\(\dfrac{1}{2}\)DC =\(\dfrac{1}{8}\)SABCD = 240\(\times\)\(\dfrac{1}{8}\)=30(cm2)
CN = BC - BN = BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC
SCPN = \(\dfrac{1}{2}\)CP\(\times\)CN= \(\dfrac{1}{2}\)\(\times\) \(\dfrac{1}{2}\)CD \(\times\) \(\dfrac{2}{3}\) BC = \(\dfrac{1}{6}\)SABCD=240\(\times\dfrac{1}{6}\)=40 (cm2)
SBMN=\(\dfrac{1}{2}\) BM\(\times\)BN =\(\dfrac{1}{2}\times\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{3}\)BC=\(\dfrac{1}{12}\)SABCD=240\(\times\)\(\dfrac{1}{12}\)=20(cm2)
Diện tích tứ giác MNPQ là:
240 - (30 + 30 + 40 + 20) = 120(cm2)
Đáp số: 120 cm2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 6 2023
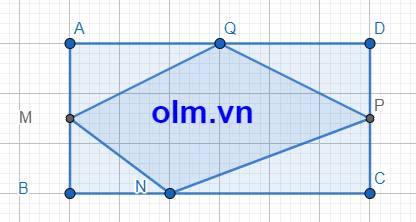
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ = \(\dfrac{1}{2}\times\) \(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{8}\)\(\times\)SABCD
SDPQ = \(\dfrac{1}{2}\)DQ\(\times\)DP = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) AD\(\times\)\(\dfrac{1}{2}\)DP = \(\dfrac{1}{8}\) \(\times\) SABCD
CN = CB - BN = CB - \(\dfrac{1}{3}\)CB = \(\dfrac{2}{3}\)CB
SCPN = \(\dfrac{1}{2}\)CP\(\times\)CN = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\) CD\(\times\)\(\dfrac{2}{3}\)CB = \(\dfrac{1}{6}\)SABCD
SBNM = \(\dfrac{1}{2}\)BN\(\times\)BM = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{2}\)AB\(\times\)\(\dfrac{1}{3}\)BC = \(\dfrac{1}{12}\)SABCD
Diện tích tứ giác MNPQ bằng: (1 - \(\dfrac{1}{8}\) - \(\dfrac{1}{8}\) - \(\dfrac{1}{6}\) - \(\dfrac{1}{12}\) )SABCD = \(\dfrac{1}{2}\)SABCD
Diện tích của tứ giác MNPQ là: 240\(\times\)\(\dfrac{1}{2}\) = 120 (cm2)
17 tháng 7 2014
SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQTính diện tích tam giác AMQ :SABQ / SABD = AQ / AD = 1/2 (hai tam giác chung đường cao hạ từ đỉnh B)SABQ = SABD x 1/2 ( chú ý: SABD=1/2 SABCD)SABQ = (216/2 ) x 1/2 = 54 (cm2)SAMQ / SABQ = AM / AB = 1/2 (hai tam giác chung đường cao hạ từ Q)SAMQ = SABQ x 1/2SAMQ = 54 x 1/2 = 27 (cm2)Tương tự, diện tích tam giác BMN :SBMN = 36 (cm2)Tương tự, diện tích tam giác CNP :SCNP = 24 (cm2)Tương tự, diện tích tam giác DPQ :SDPQ = 18 (cm2)⇒ SMNPQ = SABCD - SAMQ - SBMN - SCNP - SDPQSMNPQ = 216 - 27 - 36 - 24 - 18SMNPQ = 111 (cm2)
a: ta có; AM+MB=AB
BN+NC=BC
CP+PD=CD
DQ+QA=DA
mà AB=BC=CD=DA và AM=BN=CP=DQ
nên MB=NC=PD=QA
Xét ΔQAM vuông tại A và ΔNCP vuông tại C có
QA=NC
AM=CP
Do đó: ΔQAM=ΔNCP
b: ΔQAM=ΔNCP
=>QM=PN
Xét ΔMBN vuông tại B và ΔPDQ vuông tại D có
MB=PD
BN=DQ
Do đó: ΔMBN=ΔPDQ
=>MN=PQ
Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có
MA=NB
AQ=BM
Do đó: ΔMAQ=ΔNBM
=>MQ=MN
Ta có: ΔMAQ=ΔNBM
=>\(\widehat{AMQ}=\widehat{BNM}\)
=>\(\widehat{AMQ}+\widehat{BMN}=90^0\)
Ta có: \(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)
=>\(\widehat{QMN}+90^0=180^0\)
=>\(\widehat{QMN}=90^0\)
Xét tứ giác MNPQ có
MN=PQ
MQ=PN
Do đó: MNPQ là hình bình hành
Hình bình hành MNPQ có MN=MQ
nên MNPQ là hình thoi
Hình thoi MNPQ có \(\widehat{QMN}=90^0\)
nên MNPQ là hình vuông