Gọi E là điểm thuộc miền trong của hình vuông ABCD sao cho tam giác ABC cân tại E và có các góc đáy bằng 15 độ. Chứng minh rằng tam giác DEC đều. Giúp mk vs các bạn ơi, thank nhiều nha!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : ADCˆ=ADEˆ+EDCˆADC^=ADE^+EDC^
=> 90O=ADEˆ+15O90O=ADE^+15O
=> ADEˆ=75OADE^=75O
Tương tự ta cũng có : BCEˆ=75oBCE^=75o
Xét ΔADEΔADE và ΔBCEΔBCE có :
AD = BC (do ABCD à hình vuông)
ADEˆ=BCEˆ(=75o)ADE^=BCE^(=75o)
DE=ECDE=EC (do tam giác ECD cân tại E- gt)
=> ΔADEΔADE = ΔBCEΔBCE (c.g.c)
=> AE = BE (2 cạnh tương ứng)
Mà : AD = AE
=> ΔADEΔADE cân tại A
Xét ΔADEΔADE ta có :
ADEˆ=AEDˆ=75oADE^=AED^=75o (tính chất tam giác cân)
=> DAEˆ=180O−(ADEˆ+AEDˆ)DAE^=180O−(ADE^+AED^)
=> DAEˆ=180O−2.75O=30ODAE^=180O−2.75O=30O
Chứng minh tương tự ta có : CBEˆ=30oCBE^=30o
Có : ABEˆ=ABCˆ−CBEˆ=90O−30O=60OABE^=ABC^−CBE^=90O−30O=60O
BAEˆ=BADˆ−EADˆ=90O−30O=60OBAE^=BAD^−EAD^=90O−30O=60O
Xét ΔABEΔABE có :
ABEˆ+BAEˆ+AEBˆ=180OABE^+BAE^+AEB^=180O
=> AEBˆ=180O−2.60O=60OAEB^=180O−2.60O=60O
Thấy : ABEˆ=BAEˆ=AEBˆ=60oABE^=BAE^=AEB^=60o
=> ΔABEΔABE là tam giác đều (đpcm)
CHÚC MAY MẮN
hình tự vẽ
Vì EDC cân nên:
EDC=ECD=15
Ta có: ADE+EDC=90
=> ADE =90-15=75
Tương tự, ta có: BCE+ECD=90
=> BCE =90-15=75
Xét 2 tam giác AED và BEC có:
-góc AED=góc BEC ( đối đỉnh)
-ED=EC( tam giác EDC cân)
-góc ADE=goscBCE(cmt)
suy ra hai tam giác AED và BEC bằng nhau
==>AE=BE(2 cạnh tương ứng)
xét tam giác AEB có AE=AB=> tam giác AEB cân(đpcm)

c) Xét \(\Delta AEP\) và \(\Delta AEB\)
có: AP=AB ( p b)
góc BAE = góc PAE ( p a)
AE là cạnh chung
\(\Rightarrow\Delta AEP=\Delta AEB\left(c-g-c\right)\)
\(\Rightarrow\widehat{APE}=\widehat{ABE}=90^0\)( 2 góc tương ứng )
\(\Rightarrow\widehat{APE}=90^0\)
\(\Rightarrow AP\perp PE⋮P\)( định lí) (1)
Ta có: góc BAE + góc PAE + góc PAF + góc FAD = góc BAD
thay số: 15 + 15 + góc PAF + 30 = 90
góc PAF = 90 -15 -15 -30
góc PAF = 30
=> góc PAF = góc FAD ( = 30 độ)
Xét tam giác AFP va tam giác AFD
có: AP = AD ( p b)
góc PAF = góc FAD ( cmt)
AF là cạnh chung
\(\Rightarrow\Delta AFP=\Delta AFD\left(c-g-c\right)\)
\(\Rightarrow\widehat{APF}=\widehat{ADF}=90^0\)( 2 góc tương ứng)
\(\Rightarrow\widehat{APF}=90^0\)
\(\Rightarrow AP\perp PF⋮P\)( định lí) (2)
Từ (1); (2) => E;P;F thẳng hàng

Bài 2:
kẻ hình thang ABCD
kẻ 2 đường cao AH và BK nối B với H
xét tam giác ABH và tam giác KBH
có ^ABH = ^KBH ( 2gocs so le trong )
HB chung
=> tam giác ABH = tam giác KBH (cạnh huyền +góc nhọn )
=> AB =HK ( 2 cạnh tương ứng )
xét tam giác BKC có BC>KC ( trong tam giác vuông cạnh huyền là cạnh lớn nhất )(1)
xét tam giác AHD có AD>HD (trong tam giác vuông cạnh huyền là cạnh lớn nhất)(2)
từ (1) và (2) => BC+AD >KC+HD
ta lại có DH+DK +HK =DC
mà AB=HK (C/m )
=> DH+DK+AB =dc
ta có DC-AB = DH+DK+AB-AB= DH+DK
mà DH+DK<BC+AD(c/m)
=>DC -AB< BC+AD
vậy tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Câu 4: Cho tam giác ABC vuông tại A. Biết AB=5cm, BC=13cm. Gọi H, K lần Lượt là trung điểm của AB và BC. Tính độ dài HK
giúp mình nhoa!!

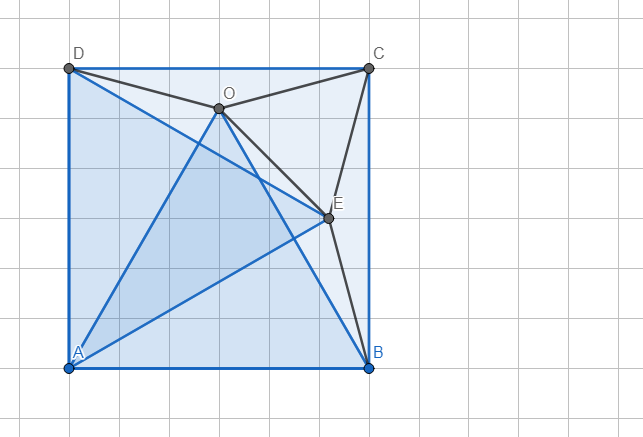
*Dựng △ADE đều.
\(\widehat{ODC}=\widehat{OCD}=15^0\Rightarrow\)△DOC cân tại O.
\(\Rightarrow OD=OC;\widehat{DOC}=180^0-2\widehat{ODC}=180^0-2.15^0=150^0\)
\(\widehat{BAE}=\widehat{CDE}=90^0-\widehat{ADE}=90^0-60^0=30^0\)
\(AB=AE=DE=DC=AD\).
\(\Rightarrow\)△DCE cân tại D, △ABE cân tại A.
\(\Rightarrow\widehat{DCE}=\widehat{ABE}=\dfrac{180^0-\widehat{BAE}}{2}=\dfrac{180^0-30^0}{2}=75^0\).
\(\Rightarrow\widehat{ECB}=\widehat{EBC}=90^0-\widehat{DCE}=90^0-75^0=15^0\)
\(\widehat{OCE}=90^0-\widehat{OCD}-\widehat{BCE}=90^0-15^0-15^0=60^0\)
△DOC và △BEC có: \(\widehat{ODC}=\widehat{EBC}=15^0;\widehat{OCD}=\widehat{ECB}=15^0;DC=BC\)
\(\Rightarrow\)△DOC=△BEC (g-c-g)
\(\Rightarrow OD=BE=OC=EC\)
\(\Rightarrow\)△OCE cân tại C mà \(\widehat{OCE}=60^0\)
\(\Rightarrow\)△OCE đều.
\(\widehat{OEB}=360^0-\widehat{OEC}-\widehat{BEC}=360^0-60^0-150^0=150^0\)
\(OE=CE=EB\Rightarrow\)△OEB cân tại E.
\(\Rightarrow\widehat{OBE}=\dfrac{180^0-\widehat{OEB}}{2}=\dfrac{180^0-150^0}{2}=15^0\)
\(\widehat{OBA}=90^0-\widehat{OBE}-\widehat{CBE}=90^0-15^0-15^0=60^0\)
Mà △OAB cân tại O \(\Rightarrow\)△OAB đều.

a, xét tam giác ABE và tam giác ACD có:
AB=AC(gt); góc A chung; AD=AE(gt)
suy ra tam giác ABE= tam giác ACD(c.g.c)
suy ra BE=CD(đpcm)
b, do 2 tam giác ABE và ACD bằng nhau
suy ra góc ABE = góc ACD
mạt khác ABC=ACB(gt)
suy ra góc EBC= góc DCB
suy ra tam giác KBC cân tại K
Lấy điểm I trong hình vuông ABCD sao cho tam giác IBC cân và có góc đáy bằng 15°. Ta tính được góc BIC = 150°
Ta có: ΔIBC = ΔEAB ⇒ IB = EB
Lại có: góc EBI = 90° - 15° - 15° = 60°
⇒ ΔEBI đều
⇒ IE = IB = IC
⇒ ΔIEC cân tại I
⇒ góc EIC = 360° - góc BIC - góc EIB = 360° - 150° - 60° = 150°
Tam giác cân IEC có góc ở đỉnh bằng 150° nên góc ICE = 15°
góc ECD = 90° - góc ICB - góc ICE = 90° - 15° - 15° = 60°
Tương tự cho góc kia: góc EDC = 60°
Vậy tam giác DEC đều.
Có làm thì mới có bài, không làm muốn có bài thì chỉ ăn cơm ăn đầu lợn