cách vẽ đồ thị hàm số kiểu gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2017
nếu như vậy thì đừng trả lời câu hỏi tào lao nữa sẽ hết bị trừ
12 tháng 2 2017
uk. cũng do mình ko biết rồi trả lời 1 lúc 3 câu hỏi ngớ ngẩn nên bị trừ 150 điểm
ad duyệt câu hỏi lâu quá nên mới tạo lại nick đây nè.
kết bạn đi, chúng ta có thể trao đổi thêm về những bài toán hay
10 tháng 2 2019
Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
10 tháng 2 2019
Đồ thị của hàm số Bài viết này không được chú giải bất kỳ nguồn tham khảo nào. ... Nếu đầu vào x là một cặp có thứ tự các số thực (x1, x2) thì đồ thị của hàm số f là tập hợp tất cả các bộ ba có thứ tự (x1, x2, f(x1, x2)), và đối với một hàm liên tục thì đó là một mặt.
AH
Akai Haruma
Giáo viên
22 tháng 7 2021
Lời giải:
a. Hình vẽ:
b. Vì điểm $A$ thuộc đths nên $A$ có tọa độ $(a,3a)$
$OA=\sqrt{a^2+(3a)^2}=2\sqrt{10}$
$\sqrt{10a^2}=2\sqrt{10}$
$10a^2=400$
$a=\pm 2$
Vậy tọa độ điểm A là $(2,6)$ hoặc $(-2,-6)$
16 tháng 12 2023
a: Để hàm số y=(2m-1)x+m-1 nghịch biến trên R thì 2m-1<0
=>2m<1
=>\(m< \dfrac{1}{2}\)
b: Thay x=-1 và y=0 vào y=(2m-1)x+m-1, ta được:
-(2m-1)+m-1=0
=>-2m+1+m-1=0
=>-m=0
=>m=0
c: Thay x=1 và y=4 vào y=(2m-1)x+m-1, ta được:
2m-1+m-1=4
=>3m-2=4
=>3m=6
=>m=2
Khi m=2 thì \(y=\left(2\cdot2-1\right)x+2-1=3x+1\)
vẽ đồ thị:
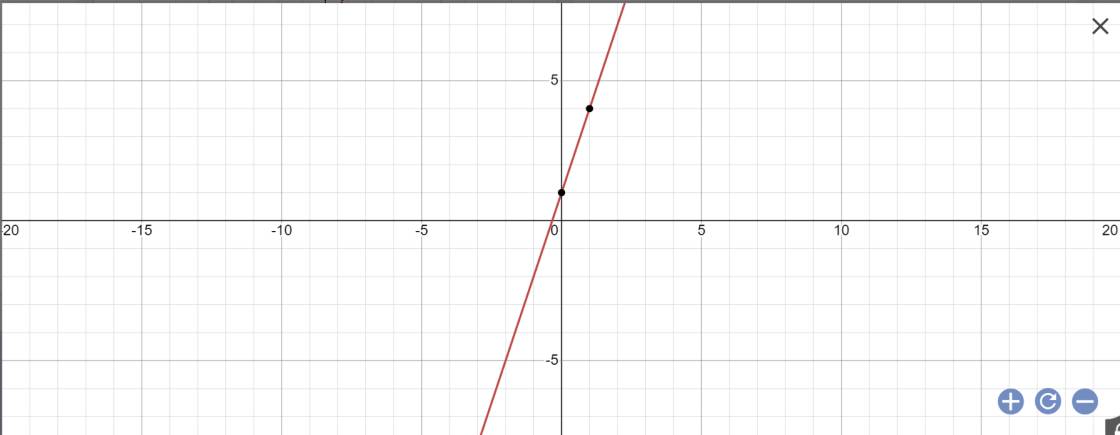
y=3x+1
=>3x-y+1=0
Khoảng cách từ O(0;0) đến đường thẳng 3x-y+1=0 là:
\(d\left(O;3x-y+1=0\right)=\dfrac{\left|0\cdot3+0\cdot\left(-1\right)+1\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{1}{\sqrt{10}}\)
CM
11 tháng 5 2018
Đồ thị hàm số y = ax2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Giả sử:
\(N_d\): Số vòng quay của bánh dẫn trong một khoảng thời gian
\(N_b\): Số vòng quay của bánh bị dẫn trong cùng khoảng thời gian
\(D_d\): Đường kính bánh dẫn
\(D_b\): Đường kính bánh bị dẫn
Vì đường kính bánh dẫn \(D_d\) gấp 2 lần đường kính bánh bị dẫn \(D_b\), ta có:
\[
\frac{D_d}{D_b} = 2
\]
Khi đó, tỷ lệ truyền động (tỷ lệ số vòng quay) là:
\[
\frac{N_b}{N_d} = \frac{D_d}{D_b} = 2
\]
=> Bánh dẫn quay được 1 vòng thì bánh bị dẫn sẽ quay được 2 vòng.
Trong 2 phút, bánh dẫn sẽ quay được:
\[
120 \times 2 = 240 \text{ vòng}
\]
Vậy trong 2 phút, bánh dẫn sẽ quay được **240 vòng**.
Kĩ năng đọc truyện ngắn chữ tình