Chứng minh 5^92 + 1 : 31
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2017
5 + 52 + 53 + 54 +55 +...............+ 590 + 591 + 592 chia hết cho 31
= ( 5 + 52 + 53 ) + ( 54 + 55 + 56 ) +...............+ ( 590 + 591 + 592 )
= ( 5.1 + 5.5 + 5. 52 ) + ( 54.1 + 54.5 + 54.52 ) +..............+ ( 590.1 + 590.5 + 590.52 )
= 5.( 1 + 5 + 52 ) + 54. ( 1 + 5 + 52 ) + ..............+ 590. ( 1 + 5 + 52 )
= 5.31 + 54.31 +..................+ 590.31
Vì 31. ( 5 + 54 +.................+ 590 ) chia hết cho 31
Nên 5 + 52 + 53 + 54 + 55 +...................+ 590 + 591 + 592 chia hết cho 31
13 tháng 12 2017
Link nó bị sao ý nhỉ, ko gửi được :v
Ta có: \(5+5^2+5^3+...+5^{90}+5^{91}+5^{92}\)
\(=\left(5+5^2+5^3\right)+...+\left(5^{90}+5^{91}+5^{92}\right)\)
\(=5\cdot\left(1+5+5^2\right)+...+5^{90}\cdot\left(1+5+5^2\right)\)
\(=5\cdot31+...+5^{90}\cdot31\)
\(=31\cdot\left(5+...+5^{90}\right)⋮31\left(dpcm\right)\)
NM
0
NT
0
31 tháng 3 2017
tach \(\frac{1}{2}=5.\frac{1}{10}\)
\(\Rightarrow A=5.\frac{1}{10}\left(7^{2012^{2015}}-3^{92^{94}}\right)⋮5\)
\(\Rightarrow A⋮5\)
TT
31 tháng 3 2017
tách 1/2 = 5.1/10
suy ra A= 5.1/10.(7^2012 ^2015-3^92^94) chia hết cho 5
suy ra a chia hết cho 5
ND
10 tháng 4 2017
7^2012^2015 có tận cùng là 1 . 3^92^94 có tận cùng là 1 . Mà 7^2012^2015 > 3^92^94 ( cái này ko có cũng đc)
=> 7^2012^2015 - 3^92^94 có tận cùng là 1-1=0
=> 1/2 . (7^2012^2015 - 3^92^94) có tận cùng là 5
=>A chia hết ( dấu chia hết ) cho 5
Vậy ....
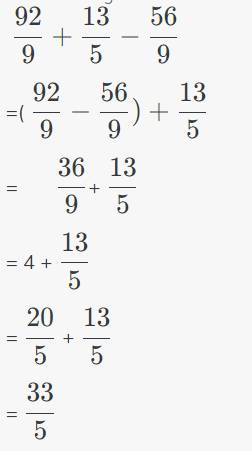
Ta có
\(A=1+5+5^2+...+5^{91}\)
\(\Rightarrow5A=5+5^2+5^3+...+5^{92}\)
\(\Rightarrow4A=5A-A=5^{92}-1\)
\(\Rightarrow5A-A+2=5^{92}+1\)
\(\Rightarrow5^{92}+1=\left(5+5^2+5^3+...+5^{92}\right)-\left(1+5+5^2+...+5^{91}\right)+2=\)
\(=\left(1+5+5^2+...+5^{92}\right)-\left(5+5^2+5^3+...+5^{91}\right)\)
Ta có
\(1+5+5^2+...+5^{92}=\left(1+5+5^2\right)+...+5^{90}\left(1+5+5^2\right)=\)
\(=31+...+5^{90}.31=31.\left(1+5^3+5^6+...+5^{90}\right)⋮31\)
Ta có
\(5+5^2+5^3+...+5^{91}=5\left(1+5+5^2\right)+...+5^{29}\left(1+5+5^2\right)=\)
\(=5.31+...+5^{29}.31=31.\left(5+5^4+5^7+...+5^{29}\right)⋮31\)
\(\Rightarrow5^{92}+1⋮31\)