Bên trong hình vuông ABCD ta đặt một hình vuông A'B'C'D' sao cho tâm hai hình vuông này trùng nhau. Chứng minh rằng trung điểm các đoạn thẳng AA', BB', CC', DD' là các đỉnh của một hình vuông có cùng tâm với hình vuông đã cho.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình tự vẽ
Gọi giao điểm của AC và BD là O => O là trung điểm của AC, BD => AO=OC;BO=OD
từ điểm O hạ OO' vuông góc với xy tại O' => OO'//DD' (2 góc đồng vị bằng nhau \(\widehat{OO'y}=\widehat{DD'y}=90^o\))
AO=OC;OO'//DD' => OC là đường trung bình của tứ giác BB'DD' => \(OC=\frac{1}{2}\left(BB'+DD'\right)\)(1)
Mặt khác: BO=OD; OO'//AA' (2 góc đồng vị bằng nhau \(\widehat{OO'y}=\widehat{AA'y}=90^o\))
=>OC là đường trung bình của tam giác AA'C => \(OC=\frac{1}{2}AA'\)(2)
Từ (1) và (2) => \(\frac{1}{2}AA'=\frac{1}{2}\left(BB'+DD'\right)\Leftrightarrow AA'=BB'+DD'\)(đpcm)



Key t chụp ở Câu hỏi của Lưu Đức Mạnh - Toán lớp 8 - Học toán với OnlineMath.Còn hình vẽ là t vẽ nha.câu c đang nghĩ~~~
C,Gọi G là giao điểm của AC và BE
=> \(AG\perp BE\) (C là trực tâm tam giác ABE)
Lại có Góc GAB= Góc GBA = 45 độ
=> tam giác ABG vuông cân
Mà A,B cố định
=> G cố định
CMTT câu b => D;F;G thẳng hàng
=> DF luôn đi qua điểm G cố định khi M di động trên AB
Vậy DF luôn đi qua điểm G cố định khi M di động trên AB

a) Viết tiếp vào chỗ chấm cho thích hợp:
- Trong hình bên có các góc vuông là:
Góc vuông đỉnh C, cạnh CM, CD. Góc vuông đỉnh D, cạnh DC, DN. Góc vuông đỉnh N, cạnh ND, NM. Góc đỉnh M, cạnh MN, MC. Goc vuông đỉnh A, cạnh AB, AE.
- M là trung điểm của đoạn thẳng BC.
- N là trung điểm của đoạn thẳng ED.
b) Xác định trung điểm I của đoạn thẳng MN, trung điểm K của đoạn thẳng CD (bằng cách đánh dấu rồi ghi tên điểm đó trên hình vẽ).
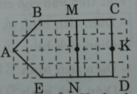
A trong hình bên có........... Góc vuông
B trong hình bên có......... Góc không vuông
C điểm m là trung điểm của đoạn thẳng
D trung điểm của đoạn thẳng.......
E điểm e ở giữa hai điểm....... Và..........,............và.........

a) ∆AME = ∆CMB (c-g-c) Þ ÐEAM = ÐBCM
Mà BCM +MBC = 900 => EAM + MBC = 900
=> AHB = 900
Vậy AE vuôn góc BC
b)Gọi O là giao điểm của AC và BD.
∆AHC vuông tại H có HO là đường trung tuyến
=> HO = \(\frac{1}{2}\)AC = \(\frac{1}{2}\)DM
=>∆DHM vuông tại H
=>DHM = 900
Chứng minh tương tự ta có: MHF = 900
Suy ra: DHM + MHF = 1800
Vậy ba điểm D, H, F thẳng hàng.

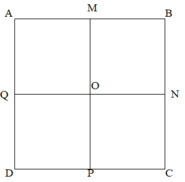
Dùng thước đo hình vuông ABCD, có độ dài cạnh là 6cm.
AM = 1 2 AB = 3cm
Chu vi hình vuông AMOQ là: AM x 4 = 3 x 4 = 12 (cm)
Đáp số: 12cm.
mình làm cách này nhé:
gọi O, I là giao 2 đường chéo của hv ABCD và A'B'C'D'
ta có :
PO//=MI
QO//=IN
suy ra tam giác POQ= tam giác MIN (c-g-c)
tương tự PON=MIQ(c-g-c)
từ đó lấy góc và cạnh sẽ được