Tìm tất cả các số tự nhiên x,y sao cho: \(\dfrac{x}{9}\)-\(\dfrac{3}{y}\)=\(\dfrac{1}{18}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LS
2
TD
1
JP
5 tháng 4 2017
\(\dfrac{x}{9}-\dfrac{3}{y}=\dfrac{1}{18}\)
\(\dfrac{x}{9}-\dfrac{1}{18}=\dfrac{3}{y}\)
\(\dfrac{2x}{18}-\dfrac{1}{18}=\dfrac{3}{y}\)
\(\dfrac{2x-1}{18}=\dfrac{3}{y}\)
\(\Rightarrow\)(2x-1).y=18.3=54
54 có các ước là: \(\pm1;\pm2;\pm3;\pm6;\pm9;\pm18;\pm27;\pm54\)
*\(\left\{{}\begin{matrix}2x-1=1\\y=54\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=2\\y=54\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=1\\y=54\end{matrix}\right.\)
*\(\left\{{}\begin{matrix}2x-1=54\\y=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=55\\y=1\end{matrix}\right.\)\(\notin\) N ( Loại)
*\(\left\{{}\begin{matrix}2x-1=2\\y=27\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=3\\y=27\end{matrix}\right.\) \(\notin\) N ( Loại )
*\(\left\{{}\begin{matrix}2x-1=27\\y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=28\\y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=14\\y=2\end{matrix}\right.\)
*\(\left\{{}\begin{matrix}2x-1=3\\y=18\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=4\\y=18\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=18\end{matrix}\right.\)
*\(\left\{{}\begin{matrix}2x-1=18\\y=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=19\\y=3\end{matrix}\right.\)\(\notin\) N ( Loại )
*\(\left\{{}\begin{matrix}2x-1=6\\y=9\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=7\\y=9\end{matrix}\right.\)\(\notin\) N ( Loại )
*\(\left\{{}\begin{matrix}2x-1=9\\y=6\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=10\\y=6\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=5\\y=6\end{matrix}\right.\)
Vậy có các cặp (x,y) t/m đề bài là : (1,54) ; (14,2) ; (2,18) ; (5,6)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2021
1.
Gọi \(d=ƯC\left(2n^2+3n+1;3n+1\right)\)
\(\Rightarrow2n^2+3n+1-\left(3n+1\right)⋮d\)
\(\Rightarrow2n^2⋮d\Rightarrow2n\left(3n+1\right)-3.2n^2⋮d\)
\(\Rightarrow2n⋮d\Rightarrow2\left(3n+1\right)-3.2n⋮d\Rightarrow2⋮d\Rightarrow\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)
\(d=2\Rightarrow3n+1=2k\Rightarrow n=2m+1\)
\(\Rightarrow n\) lẻ thì A không tối giản
\(\Rightarrow n\) chẵn thì A tối giản
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2021
2.
Giả thiết tương đương:
\(xy^2+\dfrac{x^2}{z}+\dfrac{y}{z^2}=3\)
Đặt \(\left(x;y;\dfrac{1}{z}\right)=\left(a;b;c\right)\Rightarrow a^2c+b^2a+c^2b=3\)
Ta có: \(9=\left(a^2c+b^2a+c^2b\right)^2\le\left(a^4+b^4+c^4\right)\left(c^2+a^2+b^2\right)\)
\(\Rightarrow9\le\left(a^4+b^4+c^4\right)\sqrt{3\left(a^4+b^4+c^4\right)}\)
\(\Rightarrow3\left(a^4+b^4+c^4\right)^3\ge81\Rightarrow a^4+b^4+c^4\ge3\)
\(\Rightarrow M=\dfrac{1}{a^4+b^4+c^4}\le\dfrac{1}{3}\)
\(M_{max}=\dfrac{1}{3}\) khi \(\left(a;b;c\right)=\left(1;1;1\right)\) hay \(\left(x;y;z\right)=\left(1;1;1\right)\)
NN
3
MH
4 tháng 5 2022
\(\dfrac{1}{x}+\dfrac{y}{3}=\dfrac{5}{6}\Rightarrow\dfrac{6}{6x}+\dfrac{2xy}{6x}=\dfrac{5x}{6x}\Rightarrow6+2xy=5x\)
\(\Rightarrow5x-2xy=6\Rightarrow x\left(5-2y\right)=6\)
Do \(x,y\) là số tự nhiên nên \(x\inƯ^+\left(6\right)\)
TH1: \(x=1\Rightarrow5-2y=6\Rightarrow y=-\dfrac{1}{2}\) (loại)
TH2: \(x=2\Rightarrow5-2y=3\Rightarrow y=1\) (TM)
TH3: \(x=3\Rightarrow5-2y=2\Rightarrow y=\dfrac{3}{2}\) (Loại)
TH4: \(x=6\Rightarrow5-2y=1\Rightarrow y=2\) (TM)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
4 tháng 5 2022
\(\Leftrightarrow6+2xy=5x\left(x\ne0\right)\)
\(\Leftrightarrow5x-2xy=6\Leftrightarrow x\left(5-2y\right)=6\)
\(\Leftrightarrow x=\dfrac{6}{5-2y}\)
Để x nguyên thì 5-2y phải là ước của 6
\(\Rightarrow5-2y=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow y=\left\{4;3;2;1\right\}\Rightarrow x=\left\{-2;-6;6;2\right\}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)
\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)
\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1
⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)
Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1
3\(x\) = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)
\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)
Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2
3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)
Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)
\(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)
Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2020
Hàm số xác định trên R khi và chỉ khi:
a.
\(\left(2m-4\right)x+m^2-9=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2m-4=0\\m^2-9\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
b.
\(x^2-2\left(m-3\right)x+9=0\) vô nghiệm
\(\Leftrightarrow\Delta'=\left(m-3\right)^2-9< 0\)
\(\Leftrightarrow m^2-6m< 0\Rightarrow0< m< 6\)
c.
\(x^2+6x+2m-3>0\) với mọi x
\(\Leftrightarrow\Delta'=9-\left(2m-3\right)< 0\)
\(\Leftrightarrow m>6\)
e.
\(-x^2+6x+2m-3>0\) với mọi x
Mà \(a=-1< 0\Rightarrow\) không tồn tại m thỏa mãn
f.
\(x^2+2\left(m-1\right)x+2m-2>0\) với mọi x
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(2m-2\right)=m^2-4m+3< 0\)
\(\Leftrightarrow1< m< 3\)
16 tháng 8 2023
TH1: x + y + z 0
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
= = =
= = =
⇒ x + y + z =
⇒ x + y = - z
x + z = - y
y + z = - x
Thay y + z + 1 = - x + 1
⇒ =
⇒ 2x = - x + 1
⇒ 2x + x = + 1
⇒ 3x =
⇒ x =
Thay x + z + 2 = - y + 2
⇒ =
⇒ 2y = - y + 2
⇒ 2y + y = + 2
⇒ 3y =
⇒ y =
Thay x + y - 3 = - z - 3
⇒ \frac{1}{2}$
⇒ 2z = - z - 3
⇒ 2z + z = - 3
⇒ 3z =
⇒ z =
TH2: x + y + z = 0
⇒ = = = 0
⇒ x = y = z = 0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
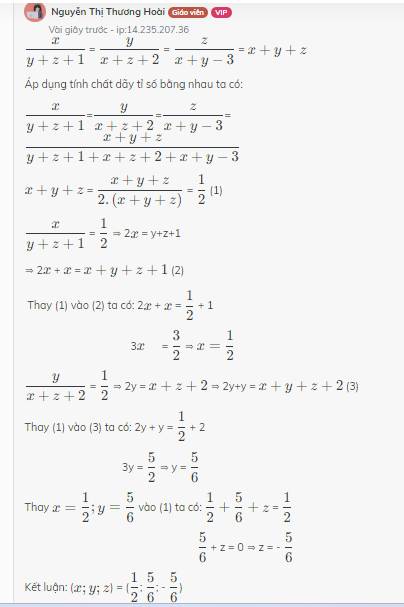
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934
HH
1
3 tháng 7 2023
=>(12-xy)/3x=5/6
=>6(12-xy)=15x
=>(12-xy)=5/2x
=>24-2xy=5x
=>5x+2xy=24
=>x(2y+5)=24
=>(x;2y+5) thuộc {(1;24); (2;12); (3;8); (4;6); (6;4); (8;3); (12;2); (24;1)}
mà x,y là các số tự nhiên
nên \(\left(x,y\right)\in\varnothing\)
AH
Akai Haruma
Giáo viên
25 tháng 5 2021
Lời giải:
\(y'=\frac{2}{3}x+m\geq 0, \forall x\in\mathbb{R}\Leftrightarrow m\geq -\frac{2}{3}x, \forall x\in\mathbb{R}\)
\(\Leftrightarrow m\geq \max (\frac{-2}{3}x), \forall x\in\mathbb{R}\)
Vì $\frac{-2}{3}x$ không có max với mọi $x\in\mathbb{R}$ nên không tồn tại $m$
\(\dfrac{x}{9}-\dfrac{3}{y}=\dfrac{1}{18}\)
=>\(\dfrac{xy-27}{9y}=\dfrac{1}{18}\)
=>\(\dfrac{2\left(xy-27\right)}{18y}=\dfrac{y}{18y}\)
=>2xy-54=y
=>2xy-y=54
=>y(2x-1)=54
mà 2x-1 lẻ
nên \(\left(2x-1;y\right)\in\left\{\left(1;54\right);\left(3;18\right);\left(9;6\right);\left(27;2\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(1;54\right);\left(2;18\right);\left(5;6\right);\left(14;2\right)\right\}\)
x/9 - 3/y = 1/18
3/y = x/9 - 1/18
3/y= 2x-1/18
y(2x-1) = 3.18 = 54
2x - 1 là ước lẻ của 54
=> 2x - 1 thuộc{3; 9; 27}
y thuộc {18; 6; 2}
2x thuộc{4; 10; 28}
x thuộc{2; 5; 14}
ta có cặp (x; y) thoả mãn là
(18; 2), (6; 5), (2; 14)