tìm x biết (x-3).(x-1)-x.(2-x)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

\(x^2\left(1+\sqrt{3}\right)x+\sqrt{3}=0\)
\(\Leftrightarrow x^2-x-\sqrt{3}x+\sqrt{3}=0\)
\(\Leftrightarrow x\left(x-1\right)-\sqrt{3}\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-\sqrt{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\sqrt{3}\end{matrix}\right.\)
\(S=\left\{1,\sqrt{3}\right\}\)
\(x^2-\left(1+\sqrt{3}\right)x+\sqrt{3}=0\)
Xét \(\Delta=b^2-4ac=\left(1+\sqrt{3}\right)^2-4.1.\sqrt{3}=4-2\sqrt{3}\)
=> Phương trình có 2 nghiệm phân biệt
\(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(1+\sqrt{3}\right)+\sqrt{4-2\sqrt{3}}}{2.1}=-1\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(1+\sqrt{3}\right)-\sqrt{4-2\sqrt{3}}}{2.1}=-\sqrt{3}\end{matrix}\right.\)

a) Tam thức bậc hai \(f\left( x \right) = 15{x^2} + 7x - 2\) có hai nghiệm phân biệt là \({x_1} = - \frac{2}{3};{x_2} = \frac{1}{5}\)
và có \(a = 15 > 0\) nên \(f\left( x \right) \le 0\) khi x thuộc đoạn \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
Vậy tập nghiệm của bất phương trình \(15{x^2} + 7x - 2 \le 0\) là \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + x - 3\) có \(\Delta = - 23 < 0\) và \(a = - 2 < 0\)
nên \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + x - 3 < 0\) có tập nghiệm là \(\mathbb{R}\)

a) Ta có đồ thị:
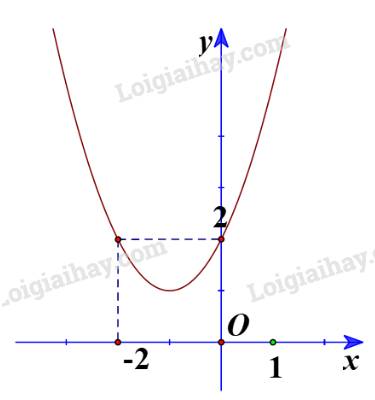
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
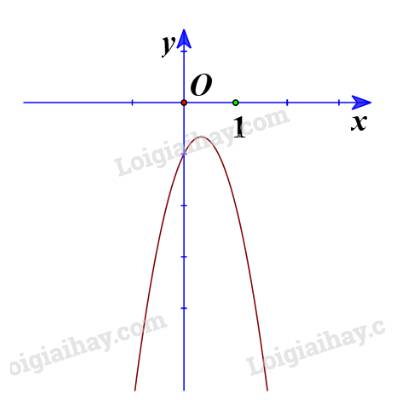
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

Hai số 1 - 2 và 1 + 2 là nghiệm của phương trình :
[x – (1 - 2 )][x – (1 + 2 )] = 0
⇔ x 2 – (1 + 2 )x – (1 - 2 )x + (1 - 2 )(1 + 2 ) = 0
⇔ x 2 – 2x – 1 = 0


Hai số -1/2 và 3 là nghiệm của phương trình :
(x + 1/2 )(x – 3) = 0 ⇔ 2 x 2 – 5x – 3 = 0
Ta có: \(\left(x-3\right)\left(x-1\right)-x\left(2-x\right)=0\)
=>\(x^2-4x+3-2x+x^2=0\)
=>\(2x^2-6x+3=0\)
=>\(x^2-3x+\dfrac{3}{2}=0\)
=>\(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{9}{4}+\dfrac{3}{2}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2-\dfrac{3}{4}=0\)
=>\(\left(x-\dfrac{3}{2}\right)^2=\dfrac{3}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{3}{2}=\dfrac{\sqrt{3}}{2}\\x-\dfrac{3}{2}=-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{3}}{2}\\x=\dfrac{3-\sqrt{3}}{2}\end{matrix}\right.\)