Một khách sạn có 50 phòng, quản lý khách sạn tính rằng, nếu mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì tất cả các phòng đều được thuê hết. Biết rằng cứ mỗi lần tăng giá phòng thêm 20 ngàn đồng thì sẽ có thêm 2 phòng trống. Hãy nh xem người quản lý khách sạn cần quyết định giá phòng bao nhiêu để thu nhập trong ngày lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt giá phòng là x. Thu nhập f(x)
bài toán được phát biểu lại dưới dạng thuần túy Toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.
Tuấn Anh Phan Nguyễn
Đặt giá phòng là x. Thu nhập f(x)
Bài toán được phát biểu lại dưới dạng thuần túy toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.

Đáp án B
Gọi x là số lần tăng tiền => Số tiền thuê một phòng là 1000000 + 50000x
Số phòng thuê được là 50 - x. Khi đó, số tiền thu được là


Ta có sơ đồ:
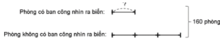
Số phần bằng nhau là:
1 + 3 = 4 (phần)
Số phòng có ban công nhìn ra biển là :
160 : 4 = 40 (phòng)
Đáp số : 40 phòng.

Nghe hay thật! 3 khách đóng 27 đồng, tên bồi ăn bớt 2 đồng, thì số tiền nộp được biểu diễn theo quan hệ dấu trừ, tức là 27-2=25 đồng đúng như số tiền phải nộp chứ có phải 27+2=29 đâu bạn.

1 đồng không biến đi đâu cả !
Sau khi trả mỗi người khách 1 đồng
=> Mỗi người khách chỉ cần đóng 9 đồng
=> Nhân với 3 người là 27 đồng.
Và cộng với 3 đồng mà tên bồi kia vừa giả.( Vì hai đồng mà tên bồi giấu nằm trong 27 đồng kia rồi )
=> 27 + 3 = 30 đồng !
Hok tốt!

Gọi x là số phòng 3 người, y là số phòng 2 người, z là số phòng 1 người, ta được hệ phương trình
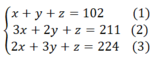
Cách 1. Dùng máy tính cầm tay.
Cách 2. Khử z để đưa về hệ phương trình hai ẩn. Trừ vế theo vế phương trình (2) cho phương trình (1) và phương trình (2) cho phương trình (3) ta được hệ phương trình
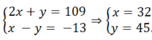
Từ đó thay vào (1) ta được z = 25.
Vậy đáp án là B.
Cách 3. Tính nhẩm.
Với phương án A, vế trái của phương trình (2) bằng 243 nên bị loại. Với phương án C, vế trái của phương trình (3) bằng 245 nên bị loại. Tương tự với phương án D, vế trái của phương trình (3) bằng 245 nên loại.
Đáp án: B
Gọi \(x>0\) là số lần tăng giá (đơn vị: 20 ngàn đồng/ngày)
Khi đó số tiền mỗi phòng là \(20+x\) (20 ngàn đồng/ngày)
Số phòng có khách thuê là \(50-2x\) (phòng)
Khi đó thu nhập trong ngày là
\(\left(20+x\right)\left(50-2x\right)\)
\(=2\left(20+x\right)\left(25-x\right)\)
\(\le2\left(\dfrac{20+x+25-x}{2}\right)^2\)
\(=1012,5\)
Dấu "=" xảy ra \(\Leftrightarrow20+x=25-x\Leftrightarrow x=\dfrac{5}{2}\)
Do đó cần tăng giá thêm \(\dfrac{5}{2}.20=50\) (ngàn đồng/ngày)
\(\Rightarrow\) Giá phòng là \(400+50=450\) (ngàn đồng/ngày)
mường thanh tầng 4 nhể : )