Tính \(\dfrac{1}{99}-\dfrac{1}{99.97}-\dfrac{1}{97.95}-...-\dfrac{1}{3.1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
2
7 tháng 7 2015
a) Ta có dãy số : 11 , 13 ,....,99
Số số hạng là :
( 99 - 11 ) : 2 + 1 = 45 ( số )
Tổng là :
( 99 + 11 ) x 45 : 2 = 2475
b) Ta có dãy số : 10,12,....,50
Số số hạng là :
( 50 - 10 ) : 2 + 1 = 21 ( số )
Tổng là :
( 50 + 10 ) x 21 : 2 = 630
KV
8 tháng 2 2023
Câu 1:
var i,n:integer;
s:longint;
begin
write('Nhap n = ');readln(n);
for i:=1 to n do
s:=s+(i*10+2);
write('S = ',s);
readln;
end.
Câu 2:
var i,n:integer;
s:real;
begin
write('Nhap n = ');readln(n);
for i:=1 to n do s:=s+1/n;
write('tong la ',s:10:2);
readln;
end.
TT
17
VH
24 tháng 5 2017
số số hạng của dãy là
( 99-1):2+1 =50(số)
tông của dãy là
(99+1)x50:2=2500
đáp số 2500
đúng thì k nhé
24 tháng 5 2017
==========================================================
SK
0
SK
0
CM
20 tháng 12 2019
a)Năm số hạng đầu: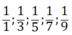 
Số hạng tổng quát của dãy số: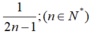 
b)Năm số hạng đầu: 1;4;7;10;13
Số hạng tổng quát của dãy số: 3n + 1(n ∈ N)
7 tháng 5 2021
...............................................................................................................................................................................................................................................? chịu thua
20 tháng 12 2019
var n,i:integer;
s:real;
begin
write('n=');readln(n);
s:=0;
for i:=1 to n do s:=s+(1/i)+(1/(i+1));
writeln(' Tong la: ',s:0:1);
readln;
end.
8 tháng 2 2021
De co cho thieu du kien la co bao nhieu so hang ko nhi ?Hay no la 1 csn lui vo han? Neu lui vo han thi lam duoc
\(\left\{{}\begin{matrix}q=4\\\dfrac{1}{u_1}+\dfrac{1}{u_2}+\dfrac{1}{u_3}+...+\dfrac{1}{u_n}+....=2\end{matrix}\right.\)
\(u_2=u_1.q;u_3=u_1.q^2;....;u_n=u_1.q^{n-1}\)
\(\Rightarrow\dfrac{1}{u_1}+\dfrac{1}{u_1.q}+\dfrac{1}{u_1.q^2}+...+\dfrac{1}{u_1.q^{n-1}}+....=2\)
\(\Leftrightarrow\dfrac{1}{u_1}\left(1+\dfrac{1}{q}+\dfrac{1}{q^2}+...+\dfrac{1}{q^{n-1}}+...\right)=2\)
Cần tính tổng trong ngoặc
\(\left\{{}\begin{matrix}u_1'=1\\q'=\dfrac{1}{q}\end{matrix}\right.\)
\(\Rightarrow S'_n=\dfrac{1}{1-q'}=\dfrac{1}{1-\dfrac{1}{4}}=\dfrac{4}{3}\)
\(\Rightarrow u_1=\dfrac{S'_n}{2}=\dfrac{4}{3.2}=\dfrac{2}{3}\)
\(\dfrac{1}{99}-\dfrac{1}{99\cdot97}-\dfrac{1}{97\cdot95}-...-\dfrac{1}{3\cdot1}\)
\(=\dfrac{1}{99}-\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{97\cdot99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{2}\left(1-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{2}\cdot\dfrac{98}{99}=\dfrac{1}{99}-\dfrac{49}{99}=-\dfrac{48}{99}=\dfrac{-16}{33}\)