Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
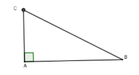
Theo hình vẽ, áp dụng hệ thức lượng trong \(\Delta ABC\left(\widehat{A}=90^o\right)\) có:
\(\frac{BC}{AC}=sin\widehat{BAC}\Leftrightarrow AC=\frac{BC}{sin\widehat{ABC}}=\frac{BC}{sin30^o}=\frac{5}{\frac{1}{2}}=10km\)
Thời gian để máy bay đạt độ cao là 5km là:
\(t=\frac{s}{v}=\frac{10}{500}=0,02h=1,12'\)
Đổi 1,5’ = 1 40 h
Sau 1,5 phút máy bay ở C
Quãng đường bay được là BC = 480. = 12km và B ^ = 25 0
Nên AC = BC. sin 25 0 = 5,1km
Vậy máy bay đạt được độ cao là 5,1km sau 1,5 phút
Đáp án cần chọn là: C
Lời giải:
Sau 2 phút bay máy bay đi được quãng đường:
$AC=600:60.2=20$ (km)
Đổi $20$ km = $20000$ m
Có: $\sin A = \frac{CB}{CA}=\frac{8500}{20000}=\frac{17}{40}$
$\Rightarrow \widehat{A}\approx 25,15^0$
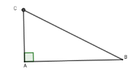
Đổi 1,2’ = 1 50 h
Sau 1,2 phút máy bay ở C
Quãng đường bay được là BC = 500. 1 50 = 10km và B ^ = 30 0
Nên AC = BC. sin 30 0 = 5km
Vậy máy bay đạt được độ cao là 5km sau 1,2 phút
Đáp án cần chọn là: B
Sau 3,6p=3/50h máy bay bay được:
500*3/50=30km
Độ cao của máy bay là:
30*sin30=15(km)
Quãng đường xiên mà máy bay bay được :
\(600.\left(1,5:60\right)=15\left(km\right)\)
Sau 15 phút, máy bay bay được độ cao :
\(x=\sin30.15=7,5\left(km\right)\)
\(t=1,5\left(phút\right)=0,025\left(giờ\right)\)
Quãng đường bay sau \(0,025\left(giờ\right)\)
\(s=v.t=600.0,025=15\left(km\right)\)
Độ cao theo phương thẳng đứng là :
\(sin30^o=\dfrac{h}{s}\Rightarrow h=s.sin30^o=15.\dfrac{1}{2}=7,5\left(km\right)\)
Để tính vận tốc trung bình của máy bay, ta cần biết quãng đường máy bay đã bay và thời gian máy bay bay. Quãng đường máy bay đã bay có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông. Ta có: quãng đường = độ cao / sin(góc nâng) = 10 km / sin(30°) = 20 km Thời gian máy bay bay là 2,4 phút = 2,4/60 = 0,04 giờ. Vận tốc trung bình của máy bay được tính bằng cách chia quãng đường máy bay đã bay cho thời gian máy bay bay: vận tốc trung bình = quãng đường / thời gian = 20 km / 0,04 giờ = 500 km/h Vậy, vận tốc trung bình của máy bay là 500 km/h.
nha bạn chúc bạn học tốt nha
Để tính vận tốc trung bình của máy bay, ta có thể làm theo các bước sau:
1. **Tính quãng đường bay**:
Giả sử máy bay bay lên theo một đường chéo tạo với phương nằm ngang một góc 32 độ. Ta có thể sử dụng công thức trong tam giác vuông.
- Độ cao (chân) của tam giác vuông: 12,363 m.
- Góc với phương nằm ngang: 32 độ.
Ta có thể tính quãng đường bay (cạnh huyền) bằng công thức:
\[
\text{Cạnh huyền} = \frac{\text{Độ cao}}{\sin(\text{góc})}
\]
Với độ cao là 12,363 m và góc là 32 độ:
\[
\text{Cạnh huyền} = \frac{12,363}{\sin(32^\circ)}
\]
Tính giá trị của \(\sin(32^\circ)\):
\[
\sin(32^\circ) \approx 0.5299
\]
Vậy:
\[
\text{Cạnh huyền} = \frac{12,363}{0.5299} \approx 23,366 \text{ m}
\]
2. **Tính vận tốc trung bình**:
- Thời gian bay: 7 phút = 7/60 giờ ≈ 0.1167 giờ.
- Vận tốc trung bình = Quãng đường / Thời gian.
\[
\text{Vận tốc trung bình} = \frac{23,366 \text{ m}}{0.1167 \text{ giờ}} \approx 200,059 \text{ m/h}
\]
3. **Chuyển đổi sang km/h**:
Vì 1 km = 1,000 m, nên ta có:
\[
\text{Vận tốc trung bình} \approx \frac{200,059}{1000} \approx 200.059 \text{ km/h}
\]
Làm tròn đến bảng đơn vị, ta có:
\[
\text{Vận tốc trung bình} \approx 200 \text{ km/h}
\]
Vậy, vận tốc trung bình của máy bay là khoảng 200 km/h.