Cho tam giác ABC có \(\widehat{B}>90^o\),điểm D nằm giữa B và C.CMR AB<AD<AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
18 tháng 5 2022
Xét ΔABD có \(\widehat{B}>90^0\)
nen AD là cạnh lớn nhất
=>AB<AD(1)
XétΔADC có \(\widehat{ADC}>90^0\)
nên AC là cạnh lớn nhất
=>AD<AC(2)
Từ (1) và (2) suy ra AB<AD<AC
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
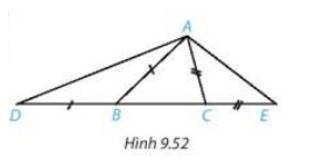
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
KH
23 tháng 1 2021
Hình ảnh minh họa , tại e k biết vẽ nhưng A và D = 90 độ và MC=CD , MB=AB . Hình dạng đúng rồi nhưng số đo góc và cạnh k đúng
HP
23 tháng 1 2021
Hình vẽ:
Từ giả thiết ta có \(\dfrac{MC}{MB}=\dfrac{CD}{AB}\left(1\right)\)
Mặt khác \(\left\{{}\begin{matrix}BA\perp AD\\CD\perp AD\end{matrix}\right.\Rightarrow BA//CD\)
\(\Rightarrow\dfrac{CD}{AB}=\dfrac{NC}{NA}\left(2\right)\) (Định lí Talet)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{MC}{MB}=\dfrac{NC}{NA}\)
\(\Rightarrow MN//AB\)
Mà \(AB\perp AD\Rightarrow MN\perp AD\)
18 tháng 3 2016
góc B > 90 độ
\(\Rightarrow\)cạnh huyền AD lớn nhất => AB < AD (1)
góc ADC > góc B = 90 độ (góc ngoài tại D của tam giác ABD)
=> góc ADC > 90 độ => cạnh huyền AC lớn nhất => AD < AC (2)
Từ (1) và (2), => AB < AD <AC (đpcm)
MA
1
HT
17 tháng 2 2016
trong tam giác ABD có góc B > 90 độ => góc B là góc lớn nhất và góc ADB <90 độ
=> AD> AB ( quan hệ góc cạnh trong tam giác) hay AB<AD (1)
có góc ADB + góc ADC = 180 độ mà góc ADB < 90 độ
=> góc ADC > 90 độ
trong tam giác ADC có góc ADC > góc ACD => AC> AD hay AD<AC (2)
từ (1) và (2) => AB< AD< AC
MA
0
HT
0
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE
CC
0