bài 24: Một chiếc thang AC được dựng vào một bức tường thẳng đứng (như hình vẽ)
a) Ban đầu là khoảng cách từ chân thang đến tường là BC=1,3m và góc tạo bởi thang với phương nằm ngang là ACB=66 độ, tính độ dài thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 4 2019
Chiều cao của thang là cạnh góc vuông đối diện với góc 63 °
Ta có: AC = AB.sinB = 6,7.sin 63 ° ≈ 6 (m)
Vậy chiều cao của cái thang đạt được so với mặt đất là 6m.
HV
7 tháng 11 2021
ta có:
nm//ac
bm=cm
=>bn=na
=>nm là đtb của tam giác bac
=>nm = ca/2=0,4
vậy khoảng cánh chân của người đứng trên bật than đối với bức tường là 0,4 m
VT
9 tháng 10 2018
a,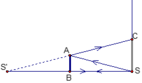 
Xét sự phản xạ ánh sáng nằm trong mặt phẳng thẳng đứng
Ta có S’ là ảnh của Svà đối xứng với S qua gương, ∆ S’SC có AB là đường trung bình nên SC = 2Ab = 2a.
Tương tự với các cạnh còn lại vậy vệt sáng trên tường là hình vuông có cạnh =2a
b,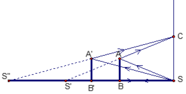 
Khi nguồn sáng S ở sát chân tườngvà di chuyển gương theo phương vuông góc với tường(đến gần hoặc ra xa tường)thì kích thước của vệt sáng không thay đổi. Luôn là hinhg vuông cạnh là 2a. Vì SC luôn bằng 2AB = 2a
Trong khoảng thời gian t gương di chuyển với vận tốc v và đi được quãng đường BB’ = vt.
Cũng trong thời gian đó ảnh S’ của S dịch chuyển với vận tốc v’ và đi được quãng đường S’S” = v’t
Theo tính chất ảnh và vật đối xứng nhau qua gương ta có:
SB’ = B’S” <=>SB + BB’ = B’S’+S’S” (1)
SB = BS’ <=> SB = BB’ + B’S’ (2)
Thay (2) và (1) ta có: BB’ + B’S’+ BB’ = B’S’+S’S” <=> 2BB’ = S’S”
Hay v’t = 2vt <=> v’ =2v
7 tháng 3 2022
Do chiếc thang đang dựa vào tòa nhà
mà chân tòa nhà là chân đường vuông góc
=>hình dáng mà chiếc thang cùng với tòa nhà tạo thành là hình tam giác vuông
áp dụng định lí pi-ta-go, ta có:
52+202=425
=>425=20.62(mình đã làm tròn con số đến số đầu tiên của phần thập phân số gốc là 20.6155281280883)
Vậy chiếc thang dài \(\approx\)20,6 m
H9
HT.Phong (9A5)
CTVHS
3 tháng 8 2023
Gọi tam giác tạo thành là tam giác ABC
Với chiếc thang là cạnh huyền AC, khoảng cách của chân thang và chân tường là BC và chiều cao của bức tường là AB:
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2+AB^2}=\sqrt{1,5^2+6^2}\approx6,2\left(m\right)\)
Độ dài của chiếc thang nhỏ:
\(A'C'=\dfrac{2}{3}\cdot AC=\dfrac{2}{3}\cdot6,2\approx4,13\left(m\right)\)
Áp dụng định lý Py-ta-go ta tìm được độ cao mà thang đặt đến:
\(A'B'=\sqrt{A'C'^2-B'C'^2}=\sqrt{4,13^2-1^2}\approx4\left(m\right)\)
Điểm cao nhất của thang cách mặt bước tường là:
\(AB-A'B'=6-4=2\left(m\right)\)
Vậy....
Hình vẽ đâu em ơi?