2X15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
0
CM
18 tháng 6 2019
Đáp án là B.
• Ta có
3 − 2 x 15 = ∑ k = 0 15 C 15 k 3 15 − k − 2 x k = ∑ k = 0 15 − 2 k 3 15 − k C 15 k x k .
Hệ số của x 7 ứng với 0 ≤ k ≤ 15, k ∈ ℕ k = 7 ⇔ k = 7 .
Vậy − 2 7 3 8 C 15 7 = − C 15 7 .3 8 .2 7 là hệ số cần tìm
CM
5 tháng 10 2018
Đáp án C.
Cách 1: Tư duy tự luận
3 − 2 x 15 = ∑ k = 0 15 C 15 k 3 15 − k − 2 x k = ∑ k = 0 15 C 15 k 3 15 − k − 2 k x k
Với 0 ≤ k ≤ 15 k ∈ ℕ
Vậy hệ số của số hạng chứa x 7 trong khai triển là C 15 7 3 8 − 2 7 = − C 15 7 3 8 2 7
Cách 2: Sử dụng máy tính cầm tay
3 − 2 x 15 = ∑ k = 0 15 C 15 k 3 15 − k − 2 k x k → f x ; k = x k g k = C 15 k 3 15 − k − 2 k
→ k = X x = 2 f X = 2 X g X = C 15 X 3 15 − X − 2 X
trong đó 0 ≤ X ≤ 15 X ∈ ℕ
Sử dụng TABLE, nhập vào máy f X = 2 X và g X = 15 C X × 3 15 − X × − 2 X . Chọn Start = 0, End = 15, Step = 1.
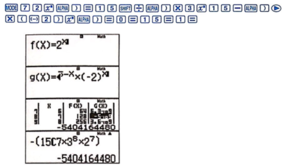
Quan sát bảng giá trị, ta thấy tại F X = 128 = 2 7 = x 7 (do x = 2 ) thì x = 7 → k = 7 và G X = − 5404164480 là hệ số của số hạng chứa x 7 trong khai triển.
Cách 3: Sử dụng công thức tính hệ số khai triển n - thức
Ta có hệ phương trình k 0 + k 1 = 15 0. k 0 + 1. k 1 = 7 ⇔ k 0 = 8 k 1 = 7
Vậy hệ số của số hạng chứa x 7 trong khai triển là
x 7 = 15 ! 7 ! .8 ! .3 8 . − 2 7 = 15 ! 15 − 7 ! .7 ! .3 8 . − 2 7 = − C 15 7 .3 8 .2 7
CM
23 tháng 9 2018
Chọn B
Ta có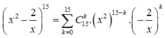 
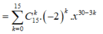
Số hạng không chứa x tương ứng với 30 - 3k = 0 => k = 10
Khi đó số hạng cần tìm là 2 10 . C 15 10 .
ND
0
BT
0
N
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 9 2018
\(B=\frac{1}{1x2x5}+\frac{1}{2x3x4}+\frac{1}{3x4x5}+...+\frac{1}{98x99x5}+\frac{1}{99x100x5}\)
\(5B=\frac{1}{1x2}+\frac{1}{2x3}+\frac{1}{3x4}+...+\frac{1}{98x99}+\frac{1}{99x100}\)
\(5B=\frac{2-1}{1x2}+\frac{3-2}{2x3}+\frac{4-3}{3x4}+...+\frac{99-98}{98x99}+\frac{100-99}{99x100}\)
\(5B=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{98}-\frac{1}{99}+\frac{1}{99}-\frac{1}{100}\)
\(5B=1-\frac{1}{100}=\frac{99}{100}\Rightarrow B=\frac{99}{500}\)
B
0
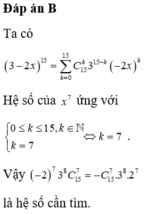
30
30