LÀM BÀI 7 GIÚP EM Ạ, NẾU DC GIÚP E BÀI 8 LUN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AM
1
Những câu hỏi liên quan
NA
1
H
24 tháng 8 2023
Bài 1:
a)
\(A=\sqrt{2}\left(\sqrt{4.2}-\sqrt{16.2}+3\sqrt{9.2}\right)\\ =\sqrt{2}\left(2\sqrt{2}-4\sqrt{2}+9\sqrt{2}\right)\\ =\sqrt{2}.7\sqrt{2}\\ =7\)
b)
\(B=\dfrac{5\left(\sqrt{6}-1\right)\left(\sqrt{6}-1\right)}{6-1}+\dfrac{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}\right)}{2-3}+\sqrt{\sqrt{2}^2-2.\sqrt{2}.\sqrt{1}+\sqrt{1}^2}\\ =\dfrac{5\left(\sqrt{6}-1\right)^2}{5}-\left(\sqrt{2}-\sqrt{3}\right)^2+\sqrt{\left(\sqrt{2}-1\right)^2}\\ =5\left(6-2\sqrt{6}+1\right)-\left(2-2\sqrt{6}+3\right)+\sqrt{2}-1\\ =30-10\sqrt{6}+5-2+2\sqrt{6}-3+\sqrt{2}-1\\ =29-8\sqrt{6}\)
25 tháng 8 2023
2:
a: \(\sqrt{x^2-2x+9}=x+2\)
=>x>=-2 và x^2-2x+9=x^2+4x+4
=>x>=-2 và -2x+9=4x+4
=>x>=-2 và -6x=-5
=>x=5/6(nhận)
b:
ĐKXĐ: x^2-4>=0 và x+2>=0
=>x>=-2 và (x>=2 hoặc x<=-2)
=>x=-2 hoặc x>=2
\(\sqrt{x^2-4}+\sqrt{x+2}=0\)
=>x^2-4=0 và x+2=0
=>x=-2
c:
ĐKXĐ: x>=1
\(\sqrt{x+3-4\sqrt{x-1}}=3\)
=>\(\sqrt{x-1-2\cdot\sqrt{x-1}\cdot2+4}=3\)
=>\(\left|\sqrt{x-1}-2\right|=3\)
=>\(\left[{}\begin{matrix}\sqrt{x-1}-2=3\\\sqrt{x-1}-2=-3\end{matrix}\right.\Leftrightarrow\sqrt{x-1}=5\)
=>x-1=25
=>x=26
d: \(\sqrt{4-8x}-4\sqrt{1-2x}+\sqrt{\dfrac{9-18x}{4}}+1=0\)
=>\(2\sqrt{1-2x}-4\sqrt{1-2x}+\dfrac{3}{2}\sqrt{1-2x}+1=0\)
=>\(1-\dfrac{1}{2}\sqrt{1-2x}=0\)
=>\(\sqrt{1-2x}=2\)
=>1-2x=4
=>2x=-3
=>x=-3/2
PG
0
M
1
30 tháng 4 2022
\(j,\left(\dfrac{-1}{2}\right)^3:1\dfrac{3}{8}-25\%\left(-6\dfrac{2}{11}\right)\)
\(=\dfrac{-1}{8}:\dfrac{11}{8}-\dfrac{1}{4}.\dfrac{-68}{11}\)
\(=\dfrac{-1}{11}-\dfrac{-17}{11}\)
\(=\dfrac{16}{11}\)
NH
0
H
8 tháng 8 2021
Bài 2 : (1) liên kết ; (2) electron ; (3) liên kết ; (4) : electron ; (5) sắp xếp electron
Bài 4 :
$\dfrac{M_X}{4} = \dfrac{M_K}{3} \Rightarrow M_X = 52$
Vậy X là crom,KHHH : Cr
Bài 5 :
$M_X = 3,5M_O = 3,5.16 = 56$ đvC
Tên : Sắt
KHHH : Fe
H
8 tháng 8 2021
Bài 9 :
$M_Z = \dfrac{5,312.10^{-23}}{1,66.10^{-24}} = 32(đvC)$
Vậy Z là lưu huỳnh, KHHH : S
Bài 10 :
a) $PTK = 22M_{H_2} = 22.2 = 44(đvC)$
b) $M_{hợp\ chất} = X + 16.2 = 44 \Rightarrow X = 12$
Vậy X là cacbon, KHHH : C
Bài 11 :
a) $PTK = 32.5 = 160(đvC)$
b) $M_{hợp\ chất} = 2A + 16.3 = 160 \Rightarrow A = 56$
Vậy A là sắt
c) $\%Fe = \dfrac{56.2}{160}.100\% = 70\%$
25 tháng 4 2020
https://www.youtube.com/channel/UC5odkiOvzz9Rvu3HUYlL2IQ?view_as=subscriber
5 tháng 10 2023
7.
1. getting - went
2. was hoping - gave
3. was living- spent
4. started - was checking in
5. was looking - saw
6. came - was showing
7. was playing - broke
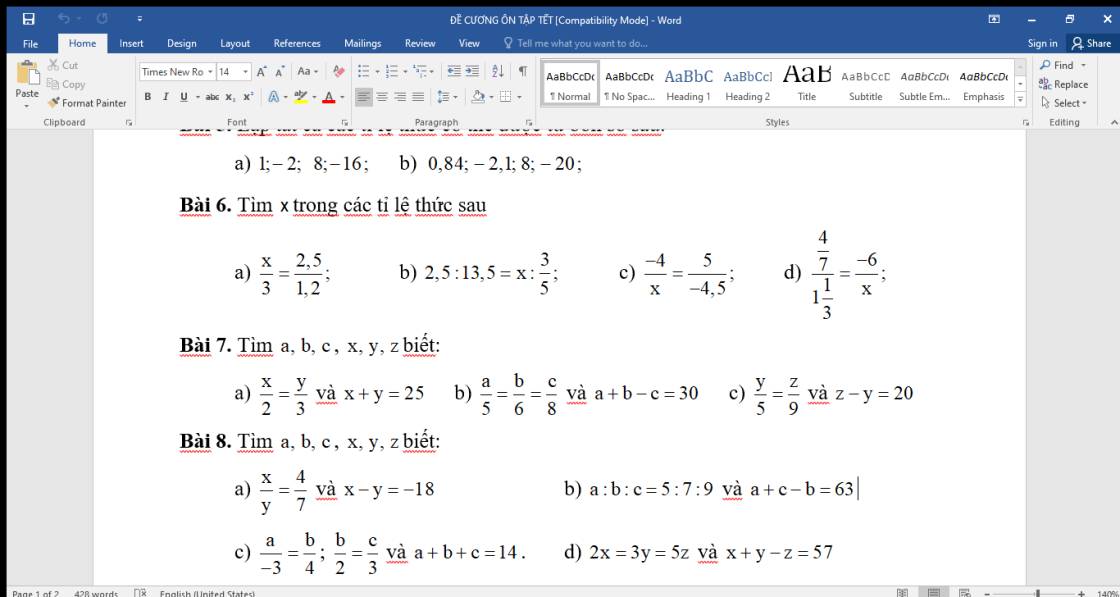giúp em làm bài 8 ạ
Bài 7 :
a) Nếu \(a< 0\Rightarrow a+\left|a\right|=0\left(vì.a+\left(-a\right)=0\right)\)
b) Nếu \(\left|a\right|-a=0\Rightarrow a\) là số không âm \(\left(...\left|a\right|=a\ge0\right)\)
c) Nếu \(a>4\Rightarrow\left|a-3\right|=a-3\left(...a-3>1>0\right)\)
d) Nếu \(\left|2a-1\right|=1-2a\Rightarrow a\le\dfrac{1}{2}\left(...1-2a\le0\Leftrightarrow a\le\dfrac{1}{2}\right)\)
Bài 8 :
a) \(\left|a\right|\ge0\) vì giá trị tuyệt đối của một số luôn không âm
b) \(\left|a\right|\ge a\)
Khi \(a\ge0\Rightarrow\left|a\right|=a\Rightarrow\left|a\right|\ge a\)
Khi \(a< 0\Rightarrow\left|a\right|=-a,-a>a\Rightarrow\left|a\right|>a\)