Cho ▲ABC cân A, đường cao AH.Kẻ phân giác của các góc AHB và góc AHC cắt AB,AC lần lượt ở D và E.
a) Tứ giác ADHE là hình gì?
b) Chứng minh DE//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2019
a, AH là đường cao của tam giác ABC (gt)
Tam giác ABC vuông cân tại A (gt)
=> AH đồng thời là đường phân giác của tam giác ABC (đl)
=> góc HAB = 1/2 góc BAC (đl)
mà góc BAC = 90 do tam giác ABC vuông cân tại A (gt)
=> góc HAB = 90 : 2 = 45 (1)
HE là phân giác của góc CHA (gt)
=> góc EHA = 1/2 góc CHA (Đl)
mà góc CHA = 90 do AH là đường cao (gt)
=> góc EHA = 90 : 2 = 45 (2)
(1)(2) => góc EHA = góc HAB = 45 mà 2 góc này sole trong
=> EH // AD (đl)
xét tứ giác ADHE
=> ADHE là hình thang
b, chứng minh đường trung bình
30 tháng 8 2021
a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{ADH}=\widehat{AEH}=90^0\)
Do đó: ADHE là hình chữ nhật
13 tháng 10 2022
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>DE=AH=6cm
b: Gọi O là giao của AH và DE
=>O là trung điểm chung của AH và DE
mà AH=DE
nên OA=OH=OD=OE
Ta có: góc OHD+góc MHD=90 độ
góc ODH+góc MDH=90 độ
mà góc OHD=góc ODH
nên góc MHD=góc MDH
=>ΔMHD cân tại M và góc MDB=góc MBD
=>ΔMBD cân tại M
=>MH=MB
=>M là trung điểm của HB
Cm tương tự, ta được N là trung điểm của HC
=>MN=1/2BC
d: \(AD\cdot AB=AH^2\)
\(AE\cdot AC=AH^2\)
Do đó: \(AD\cdot AB=AE\cdot AC\)
6 tháng 8 2021
b) Ta có: \(\widehat{DBI}=\widehat{IBC}\)(gt)
mà \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
nên \(\widehat{DBI}=\widehat{DIB}\)
hay ΔDIB cân tại D
Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, IE//BC)
mà \(\widehat{ECI}=\widehat{ICB}\)(gt)
nên \(\widehat{EIC}=\widehat{ECI}\)
hay ΔEIC cân tại E
KV
16 tháng 12 2023
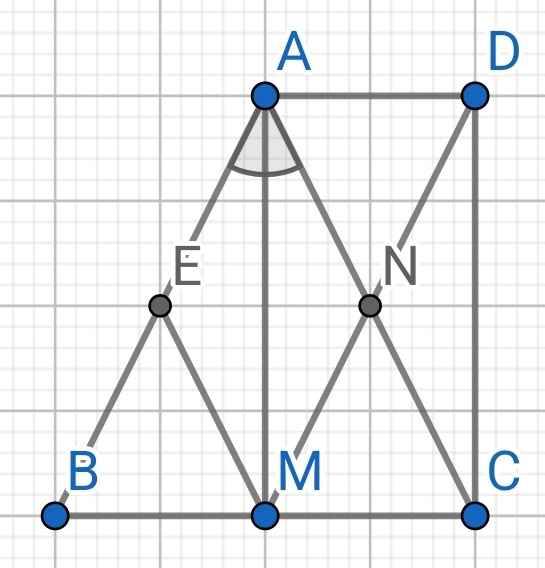a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành
21 tháng 12 2022
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>MF=ME
=>M là trung điểm của EF
=>BD=CE
13 tháng 4 2016
xét tam giác KHI có HD là phân giác trong, ta được : DI/DK=IH/KH (1)
Cũng tam giác KHI có HE là phân giác ngoài do đó: EI/EK=IH/HK(2)
1 và 2 suy ra DI/DK=EI/EK
suy ra điều phải chứng minh thôi bạn
Vì tam giác ABC cân có AH là đường cao
nên AH đồng thời là đường phân giác
\(\Rightarrow\widehat{HAB}=\widehat{HAC}\)
Ta có \(AH\perp BC\)
Mà HD và HE lần lượt là các đường phân giác
nêngócAHD=AHE
Suy ra tam giác AHD=AHE ( góc cạnh góc) ( bạn tự chứng minh)
nên AD=AE
Chứng minh AE=EH( tự chứng minh)
Mà HE=HD do tam giác AHD VÀ tam giác AHE bằng nhau
nên AE=EH=DH=AD
Vậy AEDH là hình thoi
b) Chứng minh AE=EC
AD=DB
Aps dụng tính chất đường trung bình suy ra dpcm