Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
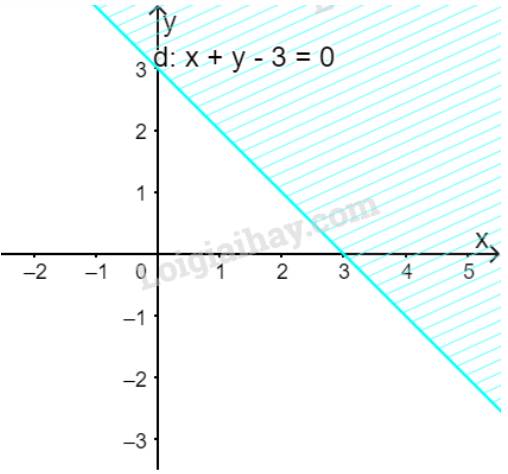
Vẽ đường thẳng \(d:x + y - 3 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 0 - 3 = - 3 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(d\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vẽ đường thẳng \(d': - 2x + y + 3 = 0\) đi qua hai điểm \(A(1; - 1)\) và \(B\left( {2;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 + 3 = 3 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
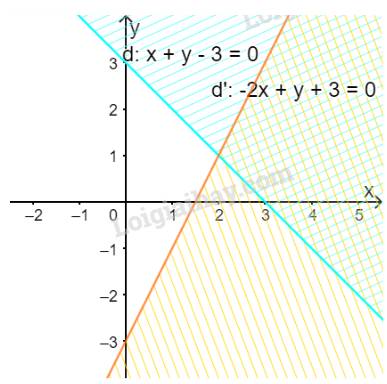
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho.
Miền góc không bị gạch được giới hạn bởi hai đường thẳng:
Đường thẳng thứ nhất đi qua hai điểm (3;0) và (0;1) nên có phương trình:
x 3 + y 1 = 1 ⇔ x + 3 y - 3 = 0
Với bờ là đường thẳng x+3y-3=0, theo hình thì phần gạch bỏ không chứa O
Do đó nửa mặt phẳng không gạch (chứa O) với bờ là đường thẳng x+3y-3=0 biểu diễn nghiệm của bất phương trình x+3y-3<0.
Đường thẳng thứ hai đi qua hai điểm (-1;0) và (0;-2) nên có phương trình
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Với bờ là đường thẳng 2x+y+2=0, theo hình thì phần gạch bỏ chứa O
Do đó nửa mặt phẳng không gạch (không chứa O) với bờ là đường thẳng 2x+y+2=0 biểu diễn nghiệm của bất phương trình 2x+y+2<0.
Miền không bị gạch là biểu diễn nghiệm bao gồm cả các đường thẳng, do đó hệ là
x + 3 y + 3 ≤ 0 2 x + y + 2 ≤ 0
Thay tọa độ của điểm O (0;0) vào các bất phương trình ta thấy O thuộc miền nghiệm của bất phương trình x + 3 y - 6 < 0 và 2 x + y + 4 > 0 .
Do đó O thuộc miền nghiệm của hệ bất phương trình x + 3 y - 6 < 0 2 x + y + 4 > 0 .
Đáp án là C.
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
Miền góc không bị gạch được giới hạn bởi hai đường thẳng:
Đường thẳng thứ nhất đi qua hai điểm (6;0) và (0;2) nên có phương trình:
x 6 + y 2 = 1 ⇔ x + 3 y - 6 = 0
Với bờ là đường thẳng x+3y-6=0 theo hình thì gạch bỏ đi phần không chứa O
Do đó nửa mặt phẳng không gạch (chứa O) với bờ là x+3y-6=0 biểu diễn nghiệm của bất phương trình x+3y-6=<0.
Đường thẳng thứ hai đi qua hai điểm (-2;0) và (0;-4) nên có phương trình:
x - 2 + y - 4 = 1 ⇔ 2 x + y + 4 = 0
Với bờ là đường thẳng 2x+y+4=0 theo hình thì gạch bỏ đi phần chứa O
Do đó nửa mặt phẳng không gạch (không chứa O) với bờ là 2x+y+4=0 biểu diễn nghệm của bất phương trình 2x+y+4<0.
Kết hợp 2 miền ta được miền góc không bị gạch là nghiệm của hệ
x + 3 y - 6 < 0 2 x + y + 4 < 0
Chọn đáp án D.
a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x - 2y = - 2\);
\({d_2}:7x - 4y = 16\)
\({d_3}:2x + y = - 4\)
Thay tọa độ điểm O vào \(x - 2y\) ta được:
\(0 - 2.0 = 0 \ge - 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x - 4y\) ta được:
\(7.0 - 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge - 4\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
b)
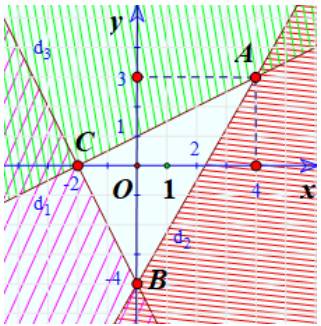
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.
và (x; y) = (-2; 1) là một nghiệm của hệ.
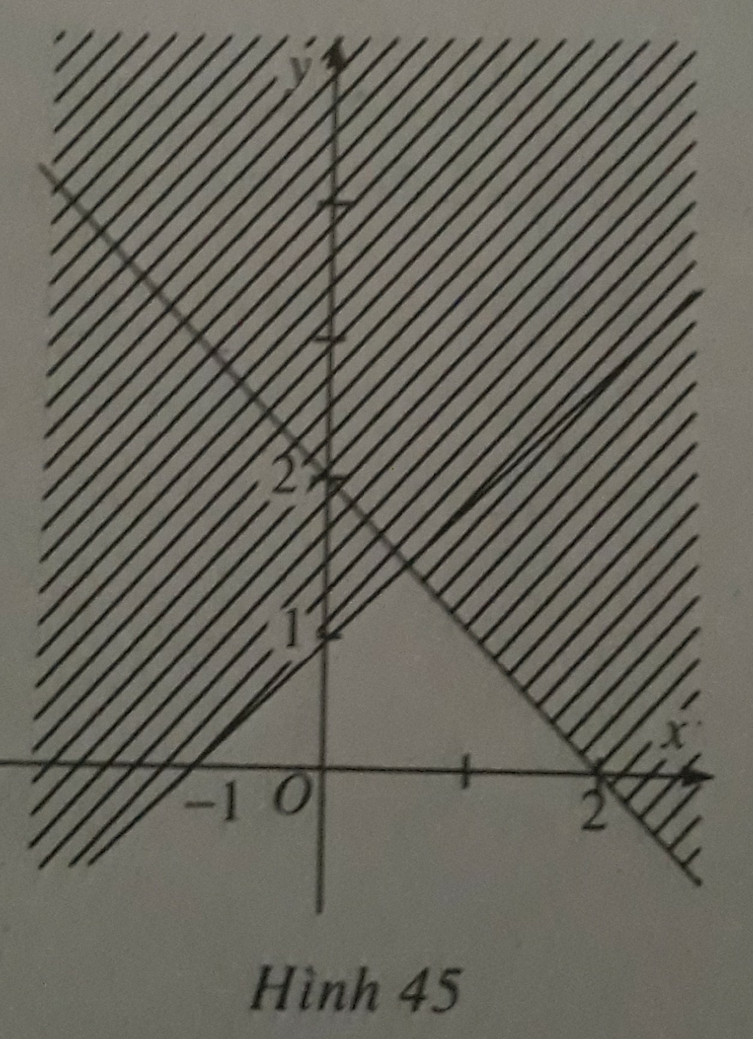
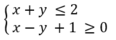và (x; y) = (1; 0) là một nghiệm của hệ.
