K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 4 2018
Số học sinh nam của trường đó là:
(1138+92);2=615(học sinh)
Số học sinh nữ của trường đó là:
1138-165=523(học sinh)
Đ/S:
22 tháng 4 2018
số học sinh nữ là
(1138 - 92) : 2 = 523 ( hs )
số học sinh nam là
(1138 + 92 ) : 2 =615( hs )
đ/s :615 hs nam
523 hs nữ
CM
6 tháng 12 2017
Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
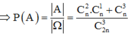
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2
T
16 tháng 5 2021
Gọi số học sinh dự tuyển của trường là (học sinh) ()
Số học sinh dự tuyển của trường là (học sinh) ()
Vì tổng số học sinh dự thi của hai trường là 750 học sinh nên ta có phương trình: (1)
Số học sinh trúng tuyển của trường là: (học sinh)
Số học sinh trúng tuyển của trường là: (học sinh)
Vì tổng số học sinh trúng tuyển của cả hai trường là học sinh nên ta có phương trình
(2)
Từ (1) và (2) ta có hệ phương trình
Vậy số học sinh dự thi của trường là học sinh
Số học sinh dự thi của trường là học sinh.
16 tháng 5 2021
1) Gọi x(km/h) là vận tốc của xe 1 ( x > 10 )
Vận tốc của xe 2 = x - 10 (km/h)
Thời gian xe 1 đi hết quãng đường AB = 160/x (km)
Thời gian xe 2 đi hết quãng đường AB = 160/(x-10) (km)
Khi đó xe 1 đến B sớm hơn xe 2 là 48 phút = 4/5 giờ nên ta có phương trình :
\(\frac{160}{x-10}-\frac{160}{x}=\frac{4}{5}\)
<=> \(\frac{160x}{x\left(x-10\right)}-\frac{160\left(x-10\right)}{x\left(x-10\right)}=\frac{4}{5}\)
=> 4x( x - 10 ) = 8000
<=> x2 - 10x - 2000 = 0 (*)
Xét (*) có Δ = b2 - 4ac = (-10)2 - 4.1.(-2000) = 100 + 8000 = 8100
Δ > 0 nên (*) có hai nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{-b+\sqrt{\text{Δ}}}{2a}=\frac{10+\sqrt{8100}}{2}=50\left(tm\right)\\x_2=\frac{-b-\sqrt{\text{Δ}}}{2a}=\frac{10-\sqrt{8100}}{2}=-40\left(ktm\right)\end{cases}}\)
Vậy vận tốc của xe 2 là 40km/h
4 tháng 6 2021
gọi vận tốc của xe thứ hai là x (km/h)
⇒t/g xe thứ hai đi là \(\dfrac{160}{x}\)(h)
vận tốc của xe thứ nhất là x+10 (km/h) (x>0)
⇒t/g của xe thứ nhất đi là \(\dfrac{160}{x+10}\left(h\right)\)
vì xe thứ nhất đến sớm hơn xe thứ hai là 48'=\(\dfrac{4}{5}h\) nên ta có pt:
\(\dfrac{160}{x}-\dfrac{160}{x+10}=\dfrac{4}{5}\)
⇔\(\dfrac{800x+8000-800x}{5x\left(x+10\right)}=\dfrac{4x^2+40x}{5x\left(x+10\right)}\)⇒4x\(^2\)+40x-8000=0
Δ=40\(^2\)-4.4.(-8000)=129600>0
⇒pt có hai nghiệm pb
x\(_{_{ }1}\)=\(\dfrac{-40+\sqrt{129600}}{8}\)=40 (TM)
x\(_2\)=\(\dfrac{-40-\sqrt{129600}}{8}\)=-50 (KTM)
vậy vận tốc của xe thứ hai là 40 km/h
24 tháng 12 2017
Số học sinh nữ của trường đó là :
523 - 114= 409 ( em )
Tổng số học sinh của trường đó là :
409+523= 932 ( em)
Số học sinh nữa chiếm số phần trăm là :
(409 : 932) x 100 % =43,88%
Đáp số : 43,88%
Gọi số học sinh của trường đó là a (với a là số nguyên dương)
Do số học sinh xếp hàng 13 dư 4 nên a chia 13 dư 4
\(\Rightarrow a=13n+4\) (với \(n\in N\)) (1)
Do số học sinh xếp hàng 17 dư 9 nên a chia 17 dư 9
\(\Rightarrow a=17m+9\) (với `m \in N\`)
\(\Rightarrow13n+4=17m+9\)
\(\Rightarrow13n+4-43=17m+9-43\)
\(\Rightarrow13n-39=17m-34\)
\(\Rightarrow13\left(n-3\right)=17\left(m-2\right)\)
Do 13 và 17 nguyên tố cùng nhau suy ra \(n-3\) chia hết 17
\(\Rightarrow n-3=17k\) (với `k \in N`)
\(\Rightarrow n=17k+3\) (2)
Từ (1) và (2) suy ra:
\(a=13.\left(17k+3\right)+4\)
\(\Rightarrow a=221k+43=5.\left(44k+8\right)+\left(k+3\right)\) (3)
Do xếp hàng 5 vừa đủ nên a chia hết cho 5 (4)
Từ (3) và (4) suy ra `k+3` chia hết cho 5
Suy ra `k=5b-3` (với `b \in N`)
Suy ra: \(a=221.\left(5k-3\right)+43=1105b-620\)
Do số học sinh của trường vào khoảng 2500 đến 3000 bạn nên:
\(2500< 1105b-620< 3000\)
\(\Rightarrow\dfrac{48}{17}< b< \dfrac{724}{221}\Rightarrow b=3\)
Vậy \(a=1105.3-620=2695\)
Trường đó có 2695 học sinh