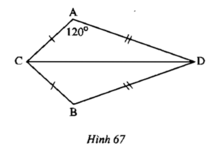
Tìm số đo góc B của hình sau; B A C D 120 ...
Đọc tiếp
Tìm số đo góc B của hình sau;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
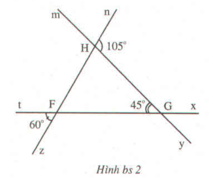
a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)
MA
2
19 tháng 10 2021
Ta có: \(\widehat{B}+\widehat{D}+\widehat{C}+\widehat{A}=360^0\)
\(\Rightarrow\widehat{B}+\widehat{D}=360^0-90^0-150^0=120^0\)
\(\Rightarrow3x=120^0\Rightarrow x=40^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=2x-2.40^0=80^0\\\widehat{D}=x=40^0\end{matrix}\right.\)
HN
1
CM
3 tháng 3 2019
ΔACD và ΔBCD có :
AC = BC (gt)
CD chung
AD = BD (gt)
⇒ ΔACD = ΔBCD (c.c.c)
⇒ góc A = góc B = 120o (hai góc tương ứng)
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
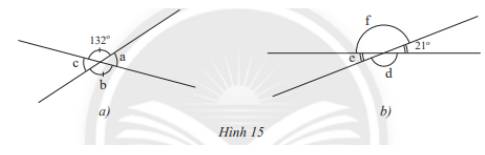
a) Ta có: b = 132\(^\circ \)( 2 góc đối đỉnh)
a + 132\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên a = 180\(^\circ \) - 132\(^\circ \) = 48\(^\circ \)
c = a = 48\(^\circ \)(2 góc đối đỉnh)
b) e = 21\(^\circ \)(2 góc đối đỉnh)
d + 21\(^\circ \) =180\(^\circ \) (2 góc kề bù) nên d = 180\(^\circ \)- 21\(^\circ \)= 159\(^\circ \)
f = d =159\(^\circ \)(2 góc đối đỉnh)
PT
1
b) 
b) 
; b) Chứng minh: OD 
AB
và x – y + z = – 49.
5 tháng 10 2015
nua chu vi hinh chu nhat la : 60:2=30
goi a,b lan luot ti so giua 2 cah 2/3 :
=>a/b=2/3=a/2=b/3 va a+b=30
adtcdts=n:
a/2=b/3=a+b/2+3=30/5=6
suy ra : a/2=6=>a=6.2=12
b/3=6=>b=6.3=18
dien tinh hinh chu nhat la :
12.18=216 ( m^2)
vay dien tinh hin chua nhat la 216 m^2
nho lik e